
已知:如图1,平面直角坐标系![]() 中,四边形OABC是矩形,点A,C的坐标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线
中,四边形OABC是矩形,点A,C的坐标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线![]() =-
=-![]() +
+![]() 交折线O-A-B于点E.
交折线O-A-B于点E.
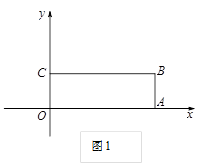
1.(1)在点D运动的过程中,若△ODE的面积为S,求S与![]() 的函数关系式,并写出自变量的取值范围;
的函数关系式,并写出自变量的取值范围;
2.(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.探究四边形DMEN各边之间的数量关系,并对你的结论加以证明;

3.(3)问题(2)中的四边形DMEN中,ME的长为____________.
1.解:(1)∵矩形OABC中,点A,C的坐标分别为![]() ,
,![]() ,
,
∴点B的坐标为![]() .
.
若直线![]() 经过点C
经过点C![]() ,则
,则![]() ;
;
若直线![]() 经过点A
经过点A![]() ,则
,则![]() ;
;
若直线![]() 经过点B
经过点B![]() ,则
,则![]() .
.
①当点E在线段OA上时,即![]() 时,(如图6)
时,(如图6)
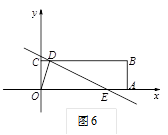
∵点E在直线![]() 上,
上,
当![]() 时,
时,![]() ,
,
∴点E的坐标为![]() .
.
∴![]()
![]() .
.
②当点E在线段BA上时,即![]() 时,(如图7)
时,(如图7)
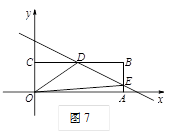
∵点D,E在直线![]() 上,
上,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
∴点D的坐标为![]() ,点E的坐标为
,点E的坐标为![]() .
.
∴![]()
![]()
![]() . 综上可得:
. 综上可得:
2.(2)DM=ME=EN=ND.
证明:如图8.

∵四边形OABC和四边形O′A′B′C′是矩形,
∴CB∥OA, C′B′∥O′A′,
即DN∥ME,DM∥NE.
∴四边形DMEN是平行四边形,且∠NDE=∠DEM.
∵矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,
∴∠DEM=∠DEN.
∴∠NDE=∠DEN.
∴ND=NE.
∴四边形DMEN是菱形.
∴DM=ME=EN=ND.
3.(3)答:问题(2)中的四边形DMEN中,ME的长为 2. 5
解析:略


科目:初中数学 来源: 题型:
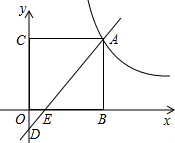 如图,在平面直角坐标系中,直y=
如图,在平面直角坐标系中,直y=| 3 |
| 2 |
| 16 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
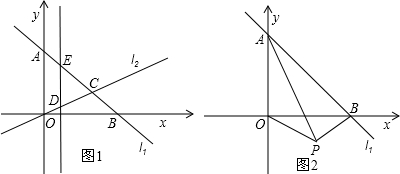
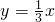 相交于点C.
相交于点C.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
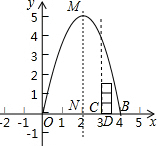 如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).
如图,在平面直角坐标系中,原点O处有一乒乓球发射器向空中发射乒乓球,乒乓球飞行路线是一条抛物线,在地面上落点落在X轴上为点B.有人在线段OB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让乒乓球落入桶内.已知OB=4米,OC=3米,乒乓球飞行最大高度MN=5米,圆柱形桶的直径为0.5,高为0.3米(乒乓球的体积和圆柱形桶的厚度忽略不计).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com