
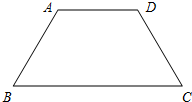
 如图,在梯形ABCD中,AD∥BC,若AB=AD=DC=2,∠A=120°,则梯形ABCD的周长为10.
如图,在梯形ABCD中,AD∥BC,若AB=AD=DC=2,∠A=120°,则梯形ABCD的周长为10. 分析 首先过点A作AE∥CD,交BC于点E,由AB=AD=DC=2,∠A=120°,易证得四边形AECD是平行四边形,△ABE是等边三角形,继而求得答案.
解答  解:过点A作AE∥CD,交BC于点E,
解:过点A作AE∥CD,交BC于点E,
∵AD∥BC,
∴四边形AECD是平行四边形,∠B=180°-∠BAD=180°-120°=60°,
∴AE=CD,CE=AD=2,
∵AB=DC,
∴△ABE是等边三角形,
∴BE=AB=2,
∴BC=BE+CE=4,
∴梯形ABCD的周长为:AB+BC+CD+AD=10.
故答案为:10.
点评 此题考查了梯形的性质、平行四边形的判定与性质以及等边三角形的判定与性质.注意准确作出辅助线是解此题的关键.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2+$\sqrt{3}$=2$\sqrt{3}$ | B. | $\sqrt{8}÷\sqrt{2}$=2 | C. | (-2a2)3=-6a6 | D. | (a+1)2=a2+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 摸球的次数m | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数n | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的概率$\frac{m}{n}$ | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,点P不与O,D重合,连接PA.设∠PAB=β,则β的取值范围是60°<β<75°.
如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,点P不与O,D重合,连接PA.设∠PAB=β,则β的取值范围是60°<β<75°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
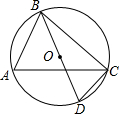 如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )
如图,⊙O的直径BD=6,∠A=60°,则BC的长度为( )| A. | $\sqrt{3}$ | B. | 3 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com