
分析 (1)若四位数abba是一个各位数字均不为零的四位对称数,它分解为两位数所表示的数和后两位数所表示的数为(10a+b)与(10b+a),则(10a+b)+10b+a=11a+11b=11(a+b),由此即可证明.
(2)三位对称数$\overline{aba}$加上其各位数字之和为100a+10b+a+2a+b=103a+11b,由0<a≤9,0≤b≤9,且103a+11b是13的倍数,用例举法即可解决问题.
解答 解:(1)若四位数abba是一个各位数字均不为零的四位对称数,
它分解为两位数所表示的数和后两位数所表示的数为(10a+b)与(10b+a),
所以(10a+b)+10b+a=11a+11b=11(a+b)
由于a、b均是整数,
所以分解后的两数的和一定能被11整除;
(2)三位对称数$\overline{aba}$加上其各位数字之和为100a+10b+a+2a+b=103a+11b,
∵0<a≤9,0≤b≤9,且103a+11b是13的倍数,
可得$\left\{\begin{array}{l}{a=1}\\{b=6}\end{array}\right.$或$\left\{\begin{array}{l}{a=3}\\{b=5}\end{array}\right.$或$\left\{\begin{array}{l}{a=5}\\{b=4}\end{array}\right.$或$\left\{\begin{array}{l}{a=7}\\{b=3}\end{array}\right.$或$\left\{\begin{array}{l}{a=8}\\{b=9}\end{array}\right.$或$\left\{\begin{array}{l}{a=9}\\{b=2}\end{array}\right.$,
∴满足条件的三位数是161或353或545或737或898或929.
点评 本题考查因式分解的应用,数字问题等知识,解题的关键是理解题意,学会用代数式解决问题,学会用例举法解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
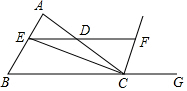 如图所示,CE为△ABC中∠BCA的角平分线,过E作BC的平行线交AC于点D,交∠ACG的平分线于点F,探究DE与DF之间的关系,并说明理由.
如图所示,CE为△ABC中∠BCA的角平分线,过E作BC的平行线交AC于点D,交∠ACG的平分线于点F,探究DE与DF之间的关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com