
 如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D
如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D 分析 (1)连接CE,根据等腰直角三角形的性质得到∠B=45°,根据切线的性质得到∠FEO=90°,得到EF∥OD,于是得到结论;
(2)过G作GN⊥BC于N,得到△GMB是等腰直角三角形,得到MB=GM,根据平行四边形的性质得到∠FCD=∠FED,根据余角的性质得到∠CGM=∠ACD,等量代换得到∠CGM=∠DEF,根据三角函数的定义得到CM=2GM,于是得到结论.
解答 解:(1)连接CE,
∵在△ABC中,AC=BC,∠ACB=90°,
∴∠B=45°,
∴∠COE=2∠B=90°,
∵EF是⊙O的切线,
∴∠FEO=90°,
∴EF∥OC,
∵DE∥CF,
∴四边形CDEF是平行四边形;
(2)过G作GN⊥BC于N,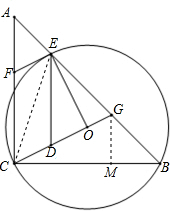
∴△GMB是等腰直角三角形,
∴MB=GM,
∵四边形CDEF是平行四边形,
∴∠FCD=∠FED,
∵∠ACD+∠GCB=∠GCB+∠CGM=90°,
∴∠CGM=∠ACD,
∴∠CGM=∠DEF,
∵tan∠DEF=2,
∴tan∠CGM=$\frac{CM}{GM}$=2,
∴CM=2GM,
∴CM+BM=2GM+GM=3,
∴GM=1,
∴BG=$\sqrt{2}$GM=$\sqrt{2}$.
点评 本题考查了切线的性质,平行四边形的判定和性质,等腰直角三角形的判定和性质,解直角三角形,正确的作出辅助线是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| 用水量(吨) | 15 | 20 | 25 | 30 | 41 |
| 户数 | 3 | 6 | 7 | 9 | 5 |
| A. | 25,27 | B. | 25,25 | C. | 30,27 | D. | 30,25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
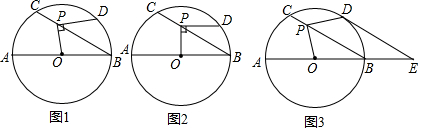
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
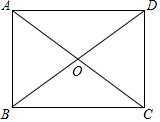 如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
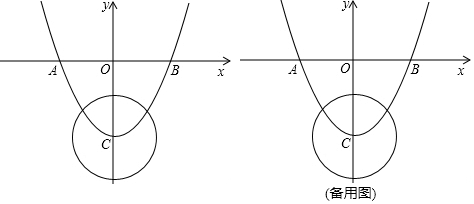
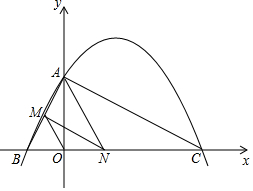 如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.查看答案和解析>>
科目:初中数学 来源:2017届江苏省启东市九年级寒假作业测试(开学考试)数学试卷(解析版) 题型:填空题
如图,点A,B在反比例函数 (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com