练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，ΔABC与ΔA’B’C’关于直线l对称，则∠B的度数为 （）

    A.30°
    B.50°
    C.90°
    D.100°

    【答案】D
    【解析】本题主要考查了轴对称的性质与三角形的内角和是180度
    由已知条件，根据轴对称的性质可得∠C=∠C′=30°，利用三角形的内角和等于180°可求答案．
    ∵△ABC与△A′B′C′关于直线l对称，
    ∴∠A=∠A′=50°，∠C=∠C′=30°；
    ∴∠B=180°-80°=100°．
    故选D
    【考点精析】根据题目的已知条件，利用三角形的内角和外角和轴对称的性质的相关知识可以得到问题的答案，需要掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角；关于某条直线对称的两个图形是全等形；如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线；两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图①所示，已知在矩形ABCD中，AB=60cm，BC=90cm，点P从点A出发，以3cm/s的速度沿AB运动；同时，点Q从点B出发，以20cm/s的速度沿BC运动．当点Q到达点C时，P、Q两点同时停止运动．设点P、Q运动的时间为t（s）．

    （1）当t=s时，△BPQ为等腰三角形；
    （2）当BD平分PQ时，求t的值；
    （3）如图②，将△BPQ沿PQ折叠，点B的对应点为E，PE、QE分别与AD交于点F、G．
    探索：是否存在实数t，使得AF=EF？如果存在，求出t的值：如果不存在，说明理由．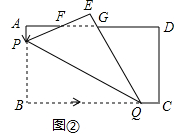

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图为两正方形ABCD、BEFG和矩形DGHI的位置图，其中G、F两点分别在BC、EH上．若AB=5，BG=3，则△GFH的面积为何？（ ）
    A.10
    B.11
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某玩具厂生产一种玩具，本着控制固定成本，降价促销的原则，使生产的玩具能够全部售出．据市场调查，若按每个玩具280元销售时，每月可销售300个．若销售单价每降低1元，每月可多售出2个．据统计，每个玩具的固定成本Q（元）与月产销量y（个）满足如下关系：

    月产销量y（个）

    …

    160

    200

    240

    300

    …

    每个玩具的固定成本Q（元）

    …

    60

    48

    40

    32

    …


    （1）每月产销量y（个）与销售单价x（元）之间的函数关系式为； 从上表可知，每个玩具的固定成本Q（元）与月产销量y（个）之间满足反比例函数关系式，求出Q与y之间的关系式；
    （2）若每个玩具的固定成本为30元，求它的销售单价是多少元？
    （3）若该厂这种玩具的月产销量不超过400个，求此时销售单价最低为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一次数学活动课上，老师带领学生去测一条南北流向的河宽，如图所示，某学生在河东岸点A处观测到河对岸水边有一点C，测得C在A北偏西31°的方向上，沿河岸向北前行20米到达B处，测得C在B北偏西45°的方向上，请你根据以上数据，帮助该同学计算出这条河的宽度．（参考数值：tan31°≈ ，sin31°≈ ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB=4，BC=2，E是AB的中点，直线l平行于直线EC，且直线l与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线l上，则DF的长为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题正确的个数是（ ）
    ①若代数式有意义，则x的取值范围为x≤1且x≠0．
    ②我市生态旅游初步形成规模，2012年全年生态旅游收入为302 600 000元，保留三个有效数字用科学记数法表示为3.03×108元．
    ③若反比例函数（m为常数），当x＞0时，y随x增大而增大，则一次函数y=﹣2x+m的图象一定不经过第一象限．
    ④若函数的图象关于y轴对称，则函数称为偶函数，下列三个函数：y=3，y=2x+1，y=x2中偶函数的个数为2个．
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，二次函数y=ax2+bx+c的图象经过点A（﹣1，0），B（0，﹣ ），C（2，0），其对称轴与x轴交于点D

    （1）求二次函数的表达式及其顶点坐标；
    （2）若P为y轴上的一个动点，连接PD，则 PB+PD的最小值为；
    （3）M（x，t）为抛物线对称轴上一动点
    ①若平面内存在点N，使得以A，B，M，N为顶点的四边形为菱形，则这样的点N共有 个；
    ②连接MA，MB，若∠AMB不小于60°，求t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知四边形ABCD是平行四边形，从下列条件：①AB=BC，②∠ABC=90°， ③AC=BD，④AC⊥BD中，再选两个做为补充，使ABCD变为正方形．下面四种组
    合，错误的是（ ）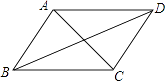

    A.①②
    B.①③
    C.②③
    D.②④

    查看答案和解析>>

    同步练习册答案