练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

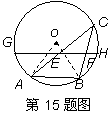
    如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点，若⊙O的半径为9，则GE+FH的最大值为           ．

     



     13.5


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    计算：(1+sin60°)-  

    查看答案和解析>>

    科目：初中数学 来源： 题型：


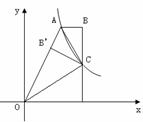
    如图，双曲线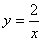（x＞0）经过四边形OABC的顶点A、C，∠ABC＝90°，OC平分OA与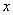轴正半轴的夹角，AB∥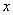轴，将△ABC沿AC翻折后得到△AB＇C，B＇点落在OA上，则四边形OABC的面积是（   ）．

       A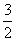．        B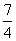．          C．2         D．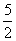

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图等腰梯形ABCD，AE是BC边上的高。已知AE=4，CE=8，则梯形ABCD的面积是（  ）A.16      B.32      C.24     D. 48

             (第3题)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


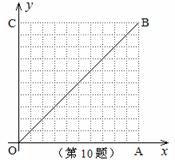
     如图，在10×10的网格中，每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点。若抛物线经过图中的三个格点，则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”。以O为坐标原点建立如图所示的平面直角坐标系，若抛物线与网格对角线OB的两个交点之间的距离为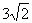，且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点，则满足上述条件且对称轴平行于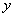轴的抛物线条数是（    ）       

    A. 16      B. 15      C. 14     D. 13

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某商场销售甲、乙两种品牌的智能手机，这两种手机的进价和售价如下表所示：

    甲

    乙

    进价（元/部）

    4000

    2500

    售价（元/部）

    4300

    3000

    该商场计划购进两种手机若干部，共需15.5万元，预计全部销售后获毛利润共2.1万元（毛利润=（售价-进价）×销售量）

    （1）该商场计划购进甲、乙两种手机各多少部？

    （2）通过市场调研，该商场决定在原计划的基础上，减少甲种手机的购进数量，增加乙种手机的购进数量，已知乙种手机增加的数量是甲种手机减少的数量的3倍，而且用于购进这两种手机的总资金不超过17.25万元，该商场怎样进货，使全部销售后获得的毛利润最大？并求出最大毛利润。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列关于x的方程一定有实数解的是（     ）

    A．                            B．

    C．                 D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


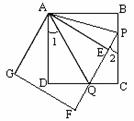
    如图，正方形ABCD的边长为3，将正方形ABCD绕点A顺时针旋转角度α（0°＜α＜90°），得到正方形AEFG，FE交线段DC于点Q，FE的延长线交线段BC于点P，连结AP、AQ．

    （1）求证：△ADQ≌△AEQ；

    （2）求证：PQ＝DQ＋PB；

    （3）当∠1=∠2时，求PQ的长．（杭十五中模拟）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     以下哪些选项可判断二次函数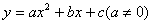与x轴有两个交点：__________（只需填上正确的序号）

    ①a+b+c=0；②b＞a+c；③b= 2a+3c；④ac＜0

    查看答案和解析>>

    同步练习册答案