
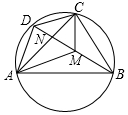
 已知圆内接四边形ABCD的对角线AC、BD交于N点,M在BD上,且∠DAN=∠BAM,∠DCN=∠BCM.求证:
已知圆内接四边形ABCD的对角线AC、BD交于N点,M在BD上,且∠DAN=∠BAM,∠DCN=∠BCM.求证:分析 (1)由圆周角定理可知∠DAN=∠DBC、∠DCN=∠DBA,结合∠DAN=∠BAM、∠DCN=∠BCM即可证出△BAM∽△CBM,根据相似三角形的性质即可得出BM2=AM•CM①,同理可得出DM2=AM•CM②,结合①②即可得出BM=DM,从而证出M为BD的中点;
(2)延长AM交圆于点P,连接CP,由圆周角定理结合∠DAN=∠BAM、∠DCN=∠BCM即可得出∠BCP=∠DBC,依据“内错角相等,两直线平行”即可得出PC∥BD,由平行线的性质即可得出$\frac{AN}{NC}=\frac{AM}{PM}$③,再通过角的转化即可得出∠APC=∠MCP,进而得出PM=CM④,结合③④即可得出$\frac{AN}{CN}=\frac{AM}{CM}$,从而证出AN•CM=AM•CN.
解答 证明:(1)根据同弧所对的圆周角相等,得∠DAN=∠DBC,∠DCN=∠DBA.
又∵∠DAN=∠BAM,∠DCN=∠BCM,
∴∠BAM=∠MBC,∠ABM=∠BCM,
∴△BAM∽△CBM,
∴$\frac{BM}{CM}=\frac{AM}{BM}$,即BM2=AM•CM.①
又∵∠DCM=∠DCN+∠NCM=∠BCM+∠NCM=∠ACB=∠ADB,∠DAM=∠MAC+∠DAN=∠MAC+∠BAM=∠BAC=∠CDM,
∴△DAM∽△CDM,
∴$\frac{DM}{CM}=\frac{AM}{DM}$,即DM2=AM•CM.②
由式①、②得:BM=DM,
∴M为BD的中点.
(2)解:如图,延长AM交圆于点P,连接CP.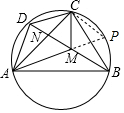
∴∠BCP=∠PAB=∠DAC=∠DBC,
∴PC∥BD,
∴$\frac{AN}{NC}=\frac{AM}{PM}$.③
又∵∠MCB=∠DCA=∠ABD,∠DBC=∠PCB,
∴∠ABC=∠MCP.
∵∠ABC=∠APC,
∴∠APC=∠MCP,
∴PM=CM.④
由式③、④得$\frac{AN}{CN}=\frac{AM}{CM}$,
∴AN•CM=AM•CN.
点评 本题考查了相似三角形的判定与性质、平行线的判定与性质、等腰三角形的性质以及圆周角定理,解题的关键是:(1)根据相似三角形的性质找出$\frac{BM}{CM}=\frac{AM}{BM}$、$\frac{DM}{CM}=\frac{AM}{DM}$;(2)根据平行线以及等腰三角形的性质找出$\frac{AN}{NC}=\frac{AM}{PM}$和PM=CM.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
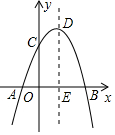 如图,在平面直角坐标系xOy中,抛物线与x轴交于点A(-1,0),B(3,0),与y轴交于点C(0,3),抛物线的顶点为D,对称轴与x轴交于点E.
如图,在平面直角坐标系xOy中,抛物线与x轴交于点A(-1,0),B(3,0),与y轴交于点C(0,3),抛物线的顶点为D,对称轴与x轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=0,b≠-1 | B. | a=0,b≠0 | C. | a≠0,b=-1 | D. | a≠0,b≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com