
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)

【答案】4
【解析】
①连接NP,MP,根据SSS定理可得△ANP≌△AMP,故可得出结论;
②先根据三角形内角和定理求出∠CAB的度数,再由AD是∠BAC的平分线得出∠1=∠2=30°,根据直角三角形的性质可知∠ADC=60°;
③根据∠1=∠B可知AD=BD,故可得出结论;
④先根据直角三角形的性质得出∠2=30°,CD=![]() AD,再由三角形的面积公式即可得出结论.
AD,再由三角形的面积公式即可得出结论.
①连接NP,MP.在△ANP与△AMP中,∵ ,∴△ANP≌△AMP,则∠CAD=∠BAD,故AD是∠BAC的平分线,故此选项正确;
,∴△ANP≌△AMP,则∠CAD=∠BAD,故AD是∠BAC的平分线,故此选项正确;
②∵在△ABC中,∠C=90°,∠B=30°,∴∠CAB=60°.
∵AD是∠BAC的平分线,∴∠1=∠2=![]() ∠CAB=30°,∴∠3=90°﹣∠2=60°,∴∠ADC=60°,故此选项正确;
∠CAB=30°,∴∠3=90°﹣∠2=60°,∴∠ADC=60°,故此选项正确;
③∵∠1=∠B=30°,∴AD=BD,∴点D在AB的中垂线上,故此选项正确;
④∵在Rt△ACD中,∠2=30°,∴CD=![]() AD,∴BC=BD+CD=AD+
AD,∴BC=BD+CD=AD+![]() AD=
AD=![]() AD,S△DAC=
AD,S△DAC=![]() ACCD=
ACCD=![]() ACAD,∴S△ABC=
ACAD,∴S△ABC=![]() ACBC=
ACBC=![]() AC
AC![]() AD=
AD=![]() ACAD,∴S△DAC:S△ABC=1:3,故此选项正确.
ACAD,∴S△DAC:S△ABC=1:3,故此选项正确.
故答案为:①②③④.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
求证:AF平分∠BAC.

【答案】证明见解析.
【解析】试题分析:先根据AB=AC,可得∠ABC=∠ACB,再由垂直,可得90°的角,在△BCE和△BCD中,利用内角和为180°,可分别求∠BCE和∠DBC,利用等量减等量差相等,可得FB=FC,再易证△ABF≌△ACF,从而证出AF平分∠BAC.
试题解析:证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高,
∴BD⊥AC,CE⊥AB(高的定义).
∴∠CEB=∠BDC=90°.
∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.
∴∠ECB=∠DBC(等量代换).
∴FB=FC(等角对等边),
在△ABF和△ACF中,
 ,
,
∴△ABF≌△ACF(SSS),
∴∠BAF=∠CAF(全等三角形对应角相等),
∴AF平分∠BAC.
【题型】解答题
【结束】
23
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.

(1)求证:CD=BE;
(2)已知CD=2,求AC的长;
(3)求证:AB=AC+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB<BC.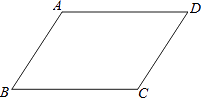
(1)利用尺规作图,在AD边上确定点E,使点E到边AB,BC的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则DE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块直角三角板![]() 放置在锐角
放置在锐角![]() 上,使得该三角板的两条直角边
上,使得该三角板的两条直角边![]() 恰好分别经过点
恰好分别经过点![]()
(1)如图①,若![]() 时,点
时,点![]() 在
在![]() 内,则
内,则![]() 度,
度,![]() ____度,
____度,![]() 度;
度;
(2)如图②,改变直角三角板![]() 的位置,使点
的位置,使点![]() 在
在![]() 内,请探究
内,请探究![]() 与
与![]() 之间存在怎样的数量关系,并验证你的结论;
之间存在怎样的数量关系,并验证你的结论;
(3)如图③,改变直角三角板![]() 的位置,使点
的位置,使点![]() 在
在![]() 外,且在
外,且在![]() 边的左侧,直接写出
边的左侧,直接写出![]() 三者之间存在的数量关系.
三者之间存在的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.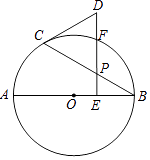
(1)求证:DC是⊙O的切线;
(2)若∠CBA=30°,射线EP交⊙O于点 F,当点 F恰好是弧BC的中点时,判断以B,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=6,AD=10,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com