
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于
于![]() ,
,![]() 为
为![]() 上一点,连接
上一点,连接![]() 交
交![]() 于
于![]() ,在
,在![]() 的延长线上取一点
的延长线上取一点![]() ,使
,使![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于
的延长线于![]() .
.
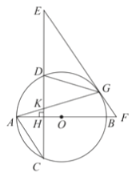
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)连接![]() ,若
,若![]() 时.
时.
①求证:![]() ;
;
②若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)①见解析,②![]()
【解析】
(1)连接OG,由EG=EK知∠KGE=∠GKE=∠AKH,结合OA=OG知∠OGA=∠OAG,根据CD⊥AB得∠AKH+∠OAG=90°,从而得出∠KGE+∠OGA=90°,据此即可得证;
(2)①由AC∥EF知∠E=∠C=∠AGD,结合∠DKG=∠CKE即可证得△KGD∽△KGE;
②连接OG,由![]() ,设
,设 ![]() 可得
可得![]() ,
,![]()
![]() 利用
利用 ![]() 得
得 ![]() 即可知 CH
即可知 CH![]()
![]() 再设
再设![]() 半径为R, 由
半径为R, 由 ![]() 可求得
可求得 ![]() 根据
根据 ![]() 知
知 ![]() 从而得出答案.
从而得出答案.
(1)如图,连接![]() .∵
.∵![]() ,
,
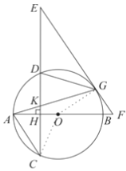
∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线.
的切线.
(2)①∵![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
又![]() ,
,
∴![]() .
.
②连接![]() ,如图所示.∵
,如图所示.∵![]() ,
,![]() ,
,
设![]() ,∴
,∴![]() ,
,![]() ,则
,则![]()
![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() .
.
在![]() 中,根据勾股定理得
中,根据勾股定理得![]() ,
,
即![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
设![]() 半径为
半径为![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得:![]() ,
,![]() ,∴
,∴![]()
在![]() 中,
中,![]() ,∴
,∴![]() ,
,
∴![]()


科目:初中数学 来源: 题型:
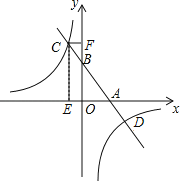
【题目】如图,已知一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反比例函数y=![]() 交于点C,D.作CE⊥x轴,垂足为E,CF⊥y轴,垂足为F.点B为OF的中点,四边形OECF的面积为16,点D的坐标为(4,﹣b).
交于点C,D.作CE⊥x轴,垂足为E,CF⊥y轴,垂足为F.点B为OF的中点,四边形OECF的面积为16,点D的坐标为(4,﹣b).
(1)求一次函数表达式和反比例函数表达式;
(2)求出点C坐标,并根据图象直接写出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:(1)4a+2b+c<0;(2)方程ax2+bx+c=0两根都大于零;(3)y随x的增大而增大;(4)一次函数y=x+bc的图象一定不过第二象限.其中正确的个数是( )
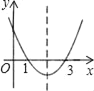
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图1,2).请根据统计图解答下列问题:
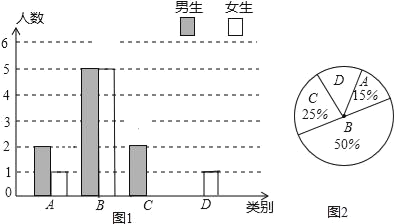
(1)本次调查中,王老师一共调查了 名学生;
(2)将条形统计图补充完整;
(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
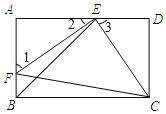
【题目】如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
(1)求证:△AEF≌△DCE;
(2)若CD=1,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
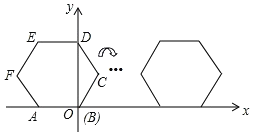
【题目】如图,将正六边形ABCDEF放置在直角坐标系内,A(﹣2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2020次翻转之后,点C的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠ABC=90°,AB=BC,点 D 是线段 AB 上的一点,连结 CD.过点 B 作 BG⊥CD,分别交 CD、CA 于点 E、F,与过点 A 且垂直于 AB 的直线相交于点 G,连结 DF,给出以下四个结论:①![]() ;②若
;②若![]()
![]() AB,则点 D 是 AB 的中点;③若
AB,则点 D 是 AB 的中点;③若![]() ,则 S△ABC=9S△BDF;④当 B、C、F、D 四点在同一个圆上时,DF=DB;其中正确的结论序号是( )
,则 S△ABC=9S△BDF;④当 B、C、F、D 四点在同一个圆上时,DF=DB;其中正确的结论序号是( )

A.①②B.①②④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
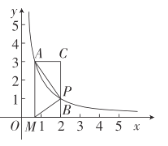
【题目】如图,在平面直角坐标系中,点A(![]() ,3)在反比例函数C:y=
,3)在反比例函数C:y=![]() (x>0)上,点P是反比例函数C:y=
(x>0)上,点P是反比例函数C:y=![]() (x>0)上-动点,连接AP,点M在x轴上,且满足MP⊥AP,垂足为P.
(x>0)上-动点,连接AP,点M在x轴上,且满足MP⊥AP,垂足为P.
(1)求反比例函数的解析式;
(2)若点P(2,n),求PM所在直线的解析式;
(3)PB⊥x轴,B为垂足,CA⊥y轴,BP的延长线交AC于点C,当△AMP与△APC相似时,请写出∠AMP与∠BMP的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
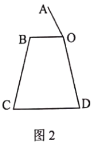
【题目】电水壶采用的是蒸汽智能感应控温原理,具有沸腾后自动断电、防干烧断电的功能.如图1,是一电水壶的实物图.当壶盖打开时,壶盖与闭合时盖面之间的夹角可以抽象为![]() (如图2),壶身侧面与底座(壶盖及底座厚度护理不计)之间的夹角可以抽象为
(如图2),壶身侧面与底座(壶盖及底座厚度护理不计)之间的夹角可以抽象为![]() (如图2)若壶嘴及手柄部分不考虑,量得壶盖和底座的直径分别为
(如图2)若壶嘴及手柄部分不考虑,量得壶盖和底座的直径分别为![]() ,
,![]() ,
,![]() .
.
(1)求底座周长比壶盖周长长多少?(结果保留![]() )
)
(2)若量得![]() ,求壶盖最高点到底座所在平面的距离.
,求壶盖最高点到底座所在平面的距离.
(结果精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .)
.)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com