
【题目】如图,![]() 中,
中,![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 中点,连接
中点,连接![]() 并延长至点
并延长至点![]() ,使得
,使得![]() ,连接
,连接![]() .
.
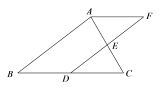
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求四边形
,求四边形![]() 的周长.
的周长.
科目:初中数学 来源: 题型:
【题目】图1是一种三角车位锁,其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时,钢条可放入底盒中(底盒固定在地面下),此时汽车可以进入车位;当车位锁上锁后,钢条按图1的方式立在地面上,以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图,经测量,钢条AB=AC=50cm,∠ABC=47°.
(1)求车位锁的底盒长BC.
(2)若一辆汽车的底盘高度为30cm,当车位锁上锁时,问这辆汽车能否进入该车位?(参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)
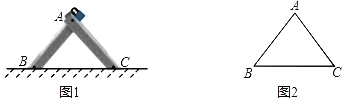
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市历史文化底蕴深厚,旅游资源丰富,钟楼、大雁塔兵马俑三个景点是人们节假日游玩的热门景点
(1)李辉从这三个景点中随机选取一个景点去游玩,求他去钟楼的概率;
(2)张慧、王丽两名同学,各自从三个景点中随机选取一个作为周末游玩的景点,用树状图或列表法求他们同时选中大雁塔的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,
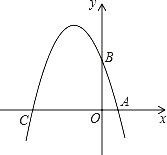
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
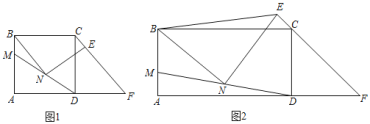
【题目】在矩形ABCD中,点F在AD延长线上,且DF=DC,M为AB边上一点,N为MD的中点,点E在直线CF上,且BN=NE.
(1)如图1,若AB=BC=6,BM=![]() AB,E为线段FC上的点,试求NE的长;
AB,E为线段FC上的点,试求NE的长;
(2)如图2,若AB<BC,E为线段FC延长线上的点,连结BE,求证:BE=![]() NE.
NE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() (其中
(其中![]() )的图像与
)的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
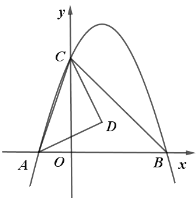
(1)点![]() 的坐标为 ,
的坐标为 ,![]()
![]() ;
;
(2)若![]() 为
为![]() 的外心,且
的外心,且![]() 与
与![]() 的面积之比为
的面积之比为![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,试探究抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
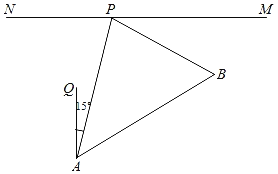
【题目】如图,在一条东西走向的公路MN的同侧有A,B两个村庄,村庄B位于村庄A的北偏东60°的方向上(∠QAB=60°),公路旁的货站P位于村庄A的北偏东15°的方向上,已知PA平分∠BPN,AP=2km,求村庄A,B之间的距离.(计算结果精确到0.01km,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目:初中数学 来源: 题型:
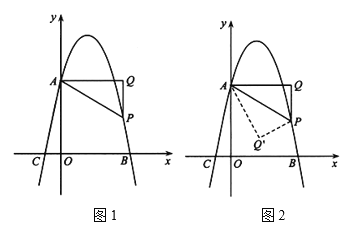
【题目】如图1,已知抛物线![]() 交y轴于点A(0,4),交x轴于点B(4,0)、C,点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作
交y轴于点A(0,4),交x轴于点B(4,0)、C,点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作![]() 于点Q,连接AP(AP不平行x轴).
于点Q,连接AP(AP不平行x轴).
(1)求抛物线的解析式;
(2)点P在抛物线上运动,若![]() ∽
∽![]() (点P与点C对应),求点P的坐标;
(点P与点C对应),求点P的坐标;
(3)如图2,若点P位于抛物线的对称轴的右侧,将![]() 沿AP对折,点Q的对应点为点
沿AP对折,点Q的对应点为点![]() ,当点
,当点![]() 落在x轴上时,求点P的坐标.
落在x轴上时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com