
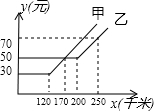
 如图,某出租车公司提供了甲、乙两种出租车费用y(元)与出租车行驶路程x(千米)之间的关系,
如图,某出租车公司提供了甲、乙两种出租车费用y(元)与出租车行驶路程x(千米)之间的关系,| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据函数图象确定出两出租车的收费,然后判断即可;
②分别求出两出租车起步价后的收费函数表达式,再求出乙比甲便宜12元的路程,即可得解;
③根据函数表达式分别求出两出租车收费60元的路程,即可得解;
④分乙比甲多10元和甲比乙多10元两种情况求解.
解答 解:①由图可知,行驶路程少于120千米,甲收费30元,乙收费50元,所收费用两出租车甲比乙便宜20元正确,故本小题正确;
②设甲行驶120千米后的函数关系式为y=kx+b,
则$\left\{\begin{array}{l}{120k+b=30}\\{170k+b=50}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{2}{5}}\\{b=-18}\end{array}\right.$,
所以,y=$\frac{2}{5}$x-18,
乙行驶200千米后的函数表达式为y=mx+n,
则$\left\{\begin{array}{l}{200m+n=50}\\{250m+n=70}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=\frac{2}{5}}\\{n=-30}\end{array}\right.$,
所以,y=$\frac{2}{5}$x-30,
若所收费用乙比甲便宜12元,
则$\frac{2}{5}$x-18-($\frac{2}{5}$x-30)=12,
∵方程有无数解,
∴x≥200时都满足,
即,行驶路程超过200千米,则所收费用乙比甲便宜12元,故本小题正确;
③甲:$\frac{2}{5}$x-18=60,
解得x=195,
乙:$\frac{2}{5}$x-30=60,
解得x=225,
∵225>195,
∴乙比甲行驶路程多,故本小题正确;
④若乙比甲多10元,则50-($\frac{2}{5}$x-18)=10,
解得x=145,
若甲比乙多10元,则$\frac{2}{5}$x-18-50=10,
解得x=195,
所以,两出租车所收费用相差10元,则行驶路程是145千米或195千米,故本小题错误;
综上所述,正确的说法是①②③共3个.
故选C.
点评 本题主要考查了函数图象的读图能力,要能根据函数图象的性质和图象上的数据分析得出函数的表达式,结合实际情况分别求解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD中,E、F分别是边AD、CD上的点,∠EBF=45°,△EDF的周长为8,则正方形ABCD的边长为( )
如图,在正方形ABCD中,E、F分别是边AD、CD上的点,∠EBF=45°,△EDF的周长为8,则正方形ABCD的边长为( )| A. | 2 | B. | 3 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1≥y2 | C. | y1>y2 | D. | y1≤y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 五子棋的比赛规则是一人执黑子,一人执白子,两人轮流出棋,每次放一个棋子在棋盘的格点处,只要有同色的五个棋子先连成一条线(横、竖、斜均可)就获得胜利.如图是两人正在玩的一盘棋,若白棋A所在点的坐标是(-2,2),黑棋B所在点的坐标是(0,4),现在轮到黑棋走,黑棋放到点C的位置就获得胜利,点C的坐标是(3,3).
五子棋的比赛规则是一人执黑子,一人执白子,两人轮流出棋,每次放一个棋子在棋盘的格点处,只要有同色的五个棋子先连成一条线(横、竖、斜均可)就获得胜利.如图是两人正在玩的一盘棋,若白棋A所在点的坐标是(-2,2),黑棋B所在点的坐标是(0,4),现在轮到黑棋走,黑棋放到点C的位置就获得胜利,点C的坐标是(3,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com