
 如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=10,则PD=5.
如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=10,则PD=5. 分析 根据角平分线的定义和平行线的性质得到∠COP=∠CPO=∠BOP,即可得出PC=OC,根据角平分线的性质得出PD=PE,求出PE,即可求出PD.
解答 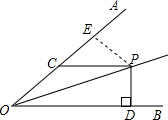 解:∵OP平分∠AOB,
解:∵OP平分∠AOB,
∴∠AOP=∠BOP,
∵PC∥OB,
∴∠CPO=∠BOP,∴∠CPO=∠AOP,
∴PC=OC,
∵PC=10,
∴OC=PC=10,
过P作PE⊥OA于点E,
∵PD⊥OB,OP平分∠AOB,
∴PD=PE,
∵PC∥OB,∠AOB=30°
∴∠ECP=∠AOB=30°
在Rt△ECP中,PE=$\frac{1}{2}$PC=5,
∴PD=PE=5,
故答案为:5.
点评 本题主要考查了含30°角的直角三角形的性质,角平分线的性质,平行线的性质的应用,注意:角平分线上的点到角的两边距离相等.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 [背景知识]数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a-b|,若a>b,则可简化为AB=a-b;线段AB的中点M表示的数为$\frac{a+b}{2}$.
[背景知识]数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a-b|,若a>b,则可简化为AB=a-b;线段AB的中点M表示的数为$\frac{a+b}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22),若圈出的9个数中,最大数与最小数的积为192,则这9个数的和为( )
如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置相邻的9个数(如6,7,8,13,14,15,20,21,22),若圈出的9个数中,最大数与最小数的积为192,则这9个数的和为( )| A. | 32 | B. | 126 | C. | 135 | D. | 144 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com