
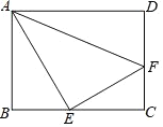
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E是BC边上的一个动点(不与点B.C重合),连结AE,并作EF⊥AE,交CD边于点F,连结AF.设BE=x,CF=y.
(1)求证:△ABE∽△ECF;
(2)当x为何值时,y的值为2;
【答案】(1)见解析;(2)x的值为2或6时,y的值为2
【解析】
(1)①先判断出∠BAE=∠CEF,即可得出结论;
(2)利用的相似三角形得出比例式即可建立x,y的关系式,代入即可;
(1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=90°.
∵AE⊥EF,
∴∠AEF=90°=∠B.
∴∠BAE+∠AEB=90°,
∠FEC+∠AEB=90°,
∴∠BAE=∠CEF.
又∵∠B=∠C,
∴△ABE∽△ECF.
②∵△ABE∽△ECF.
∴![]() ,
,
∵AB=6,BC=8,BE=x,CF=y,EC=8x,
∴![]() .
.
∴y=![]() x2+
x2+![]() x.
x.
∵y=2,![]() x2+
x2+![]() x=2,
x=2,
解得 x1=2,x2=6.
∵0<x<8,
∴x的值为2或6.


科目:初中数学 来源: 题型:
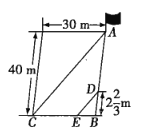
【题目】如图,在一个长40m,宽30m的长方形小操场上,王刚从A点出发,沿着A→B→C的路线以3m/s的速度跑向C地.当他出发4s后,张华有东西需要交给他,就从A地出发沿王刚走的路线追赶,当张华跑到距B地![]() m的D处时,他和王刚在阳光下的影子恰好重叠在同一条直线上.此时,A处的小旗在阳光下的影子也恰好落在对角线AC上.求:
m的D处时,他和王刚在阳光下的影子恰好重叠在同一条直线上.此时,A处的小旗在阳光下的影子也恰好落在对角线AC上.求:
(1)他们的影子重叠时,两人相距多少米(DE的长)?
(2)张华追赶王刚的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为16元的日用品,销售一段时间后,为了获取更多利润, 商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件; 若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x( 元/件)的一次函数.
(1)试求y与x之间的函数关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
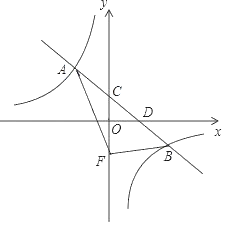
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y=![]() (k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式﹣![]() x+b>
x+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
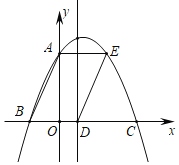
【题目】如图,抛物线y=ax2+bx+![]() 与y轴交于点A,与x轴交于点B、C,连结AB,以AB为边向右做平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则平行四边形的面积为_____.
与y轴交于点A,与x轴交于点B、C,连结AB,以AB为边向右做平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则平行四边形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,O为坐标原点,设点P的坐标为(x,y),当x<0时,点P的变换点P′的坐标为(y,﹣x);当x≥0时,点P的变换点P'的坐标为(﹣x,y).
(1)点A(1,2)的变换点A'的坐标是 ;
(2)点B(﹣2,3)的变换点B′在反比例函数y=![]() 的图象上,则k= ,∠BOB'的大小是 °;
的图象上,则k= ,∠BOB'的大小是 °;
(3)点P在抛物线y=﹣(x﹣2n)2+3上,点P的变换P′的坐标是(﹣4,﹣n),求n的值.
(4)点P在抛物线y=﹣x2﹣4x+1的图象上,以线段PP′为对角线作正方形PMP'N,设点P的横坐标为m,当正方形PMP′N的对角线垂直于x轴时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
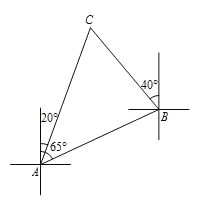
【题目】如图,一艘船由A港沿北偏东65°方向航行![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
求:(1)∠C的度数;
(2)A,C两港之间的距离为多少km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副扑克牌中点数为“2”、“3”、“4”、“6”的四张牌背面朝上洗匀,先从中抽出1张牌,记录下牌面点数为x,再从余下的3张牌中抽出1张牌,记录下牌面点数为y.设点P的坐标为(x,y).
(1)请用表格或树状图列出点P所有可能的坐标.
(2)求点P在抛物线y=x2+x上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com