【题目】如图，四边形ABCD是矩形，把矩形沿AC折叠，点B落在点E处，AE与DC的交点为O，连接DE．
（1）求证：△ADE≌△CED；
（2）求证：DE∥AC．
【答案】（1）证明见解析；（2）证明见解析.
【解析】试题分析：（1）根据矩形的性质和折叠对称的性质，由SSS可证明ADE≌CED.
（2）根据全等的性质和折叠对称的性质，可求得∠OAC =∠DEA，从而根据平行的判定得出结论.
试题解析：（1）∵ 四边形ABCD是矩形，∴AD=BC，AB=CD.
又∵AC是折痕，∴BC =" CE" =" AD" ，AB =" AE" =" CD" .
又∵DE = ED，∴ΔADE ≌ΔCED（SSS）.
（2）∵ΔADE ≌ΔCED，∴∠EDC =∠DEA.
又∵ΔACE与ΔACB关于AC所在直线对称，∴∠OAC =∠CAB.
又∵∠OCA =∠CAB，∴∠OAC =∠OCA.
∴2∠OAC = 2∠DEA. ∴∠OAC =∠DEA.
∴DE∥AC.
科目：初中数学 来源： 题型：
【题目】如图，ABCD是正方形，G是BC上（除端点外）的任意一点，DE⊥AG于点E，BF∥DE，交AG于点F．下列结论不一定成立的是【 】
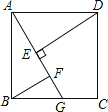
A．△AED≌△BFA B．DE﹣BF=EF C．△BGF∽△DAE D．DE﹣BG=FG
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】填空或填写理由．
（1）如图甲，∵∠ =∠ （已知）；
∴AB∥CD（ ）
（2）如图乙，已知直线a∥b，∠3=80°，求∠1，∠2的度数．
解：∵a∥b，（ ）
∴∠1=∠4（ ）
又∵∠3=∠4（ ）
∠3=80°（已知）
∴∠1=（ ）（等量代换）
又∵∠2+∠3=180°
∴∠2=（ ）（等式的性质）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在信息快速发展的社会，“信息消费”已成为人们生活的重要部分．我市区机抽取了部分家庭，调查每月用于信息消费的金额，数据整理成如图所示的不完整统计图．已知A、B两组户数直方图的高度比为1：5，请结合图中相关数据回答下列问题：
（1）A组的频数是 ，本次调查样本的容量是 ；
（2）补全直方图（需标明各组频数）；
（3）若该社区有1500户住户，请估计月信息消费额不少于300元的户数是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点A从点（1，0）出发，以1个单位长度/秒的速度沿x轴向正方向运动，以O、A为顶点作菱形OABC，使点B、C在第一象限内，且∠AOC=60°，点P的坐标为（0，3），设点A运动了t秒，求：
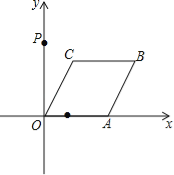
（1）点C的坐标（用含t的代数式表示）；
（2）点A在运动过程中，当t为何值时，使得△OCP为等腰三角形？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对
， 
定义一种新运算
，规定
(其中
， 
均为非零常数)，这里等式右边是通常的四则运算，例： 
.
已知
， 
.
(1)求
， 
的值；
(2)若关于m的不等式组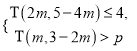
恰好有3个整数解，求实数
的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知一次函数y=kx﹣4k+5的图象与反比例函数y= 
（x＞0）的图象相交于点A（p，q）．当一次函数y的值随x的值增大而增大时，p的取值范围是 ．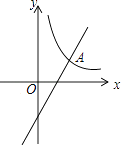 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为(3， 
)，点C的坐标为(
，0)，点P为斜边OB上的一个动点，则PA＋PC的最小值为( )
A. 
B. 
C. 
D. 2 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
