
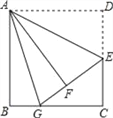
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx+b������A��2��0����B��0��1��������P��x���������ϵĶ��㣬����P��PC��x�ᣬ��ֱ��AB�ڵ�C����OA��ACΪ�߹���OACD�����P�ĺ�����Ϊm��
��1����ֱ��AB�ĺ�������ʽ��
��2�����ı���OACDǡ�����Σ������m��ֵ��
��3���ڣ�2���������£�y������������Ƿ���ڵ�Q������CQ��ʹ�á�OQC+��ODC=180�㣮�����ڣ�ֱ��д�����з��������ĵ�Q�����꣬�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��A��2��0����B��O��1������y=kx+b��
�ɵ� ![]() �����
����� 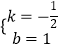 ��
��
��ֱ��AB�ĺ�������ʽΪy=�� ![]() x+1
x+1
��2��
�⣺��OACD�����Σ�
��AC=OA=2��
��PC��x�ᣬ��ֱ��AB�ڵ�C��
��C��m���� ![]() m+1����
m+1����
�ࣨ2��m��2+���� ![]() m+1��2=22��
m+1��2=22��
���m1= ![]() ��m2=
��m2= ![]()
��3��
�⣺�ɣ�2�����m1= ![]() ��m2=
��m2= ![]() ����C����ֱ��AB�ϣ�
����C����ֱ��AB�ϣ�
��C�������� ![]() ����
���� ![]() ����
���� ![]() ��
�� ![]() ����
����
��OACD������
���D=��OAC��
Ҫʹ��OQC+��ODC=180�㣬������OQC+��OAC=180�㣬
���ı���QOAC�ĶԽǻ�����
���QOA+��QCA=180�㣬
�ߡ�QOA=90�㣬
���QCA=90�㣬
��QC��AB��
��Q��0��n����
��ֱ��QC�Ľ���ʽΪy=2x+n��
��C������ֱ����y=2x+n���ɵé� ![]() =2��
=2�� ![]() +n��
+n�� ![]() =2��
=2�� ![]() +n��
+n��
���n=��4+2 ![]() ��n=��4��2
��n=��4��2 ![]() ����ȥ����
����ȥ����
���Q��������0����4+2 ![]() ����
����
���Ͽ�֪�������������ĵ�Q��������Ϊ��0����4+2 ![]() ��
��
����������1���ѵ�A��2��0����B��0��1������ֱ��y=kx+b�ⷽ�̿ɵã���2���������ε����ʵõ�AC=2���ɵ�C��m���� ![]() m+1���õ�AP=|2��m|��CP=��
m+1���õ�AP=|2��m|��CP=�� ![]()


 ��ѧ�����ϵ�д�
��ѧ�����ϵ�д� �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ12��������ABCD�У�E�DZ�CD���е㣬����ADE��AE��������AFE���ӳ�EF��BC�ڵ�G.��BG�ij�Ϊ��������
A. 5 B. 4 C. 3 D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ��Ϊ8��B��������һ�㣬��AB=14������P�ӵ�A��������ÿ��5����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮
![]()
��1��д�������ϵ�B��ʾ���� ����P��ʾ���� ���ú�t�Ĵ���ʽ��ʾ����
��2������H�ӵ�B��������ÿ��3����λ���ȵ��ٶ����������������˶�������P��Hͬʱ�������ʵ�P�˶�������ʱ�ϵ�H��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD����AB��4��BC��2.����������ƽ��ֱ������ϵ����ʹAB��x��������C��y�����������A������Ϊ(��3��0)�����B��C��D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B�ֱ�Ϊ�����ϵ����㣬A���Ӧ����Ϊ��20��B���Ӧ����Ϊ100��
![]()
��1����д����A��B���������ȵĵ�M����Ӧ������ ����
��2������һֻ��������P��B����������6��λ/����ٶ������˶���ͬʱ��һֻ��������Qǡ�ô�A���������4��λ/����ٶ������˶���x�����ֻ���������������ϵ�C�����������з������x����ָ����C��ʾ������
��3��������������P��B�����ʱ����6��λ/����ٶ������˶���ͬʱ��һֻ��������Qǡ�ô�A���������4��λ/����ٶ�Ҳ�����˶���y�����ֻ���������������ϵ�D�����������з������y��ָ����D��ʾ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�������������ȱˮ�Ĺ���֮һ��Ϊ�˳�������Լ��ˮ������������С���������ڰ��50��ͬѧ�У����������10��ͬѧ��ͥ��һ����¾���ˮ������λ��t����������������������µ�����ͳ��ͼ
��1������10���������ݵ�ƽ��������������λ����
��2�������������ݣ�����С�����ڰ�50��ͬѧ��ͥ���¾���ˮ��������7 t��Լ�ж��ٻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD��PΪ����AB�ϵ�һ�㣬��BPΪ����������BPEF��ʹ��F���߶�CB���ӳ����ϣ�����EA��EC��
������ͼ1������P���߶�AB���ӳ����ϣ���֤��EA=EC��
������ͼ2������P���߶�AB���е㣬����AC���жϡ�ACE����״����˵�����ɣ�
������ͼ3������P���߶�AB�ϣ�����AC����EPƽ�֡�AECʱ����AB=a��BP=b����a��b����AEC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ1����A��O��B������ֱ��MN�ϣ��ֽ�����OA�Ƶ�O��˳ʱ�뷽����ÿ��2����ٶ���ת��ͬʱ����OB�Ƶ�O����ʱ�뷽����ÿ��4����ٶ���ת����ͼ2������תʱ��Ϊt��0���t��90�룩��
��1���ú�t�Ĵ���ʽ��ʾ��MOA�Ķ�����
��2�����˶������У�����AOB�ڶ��δﵽ60��ʱ����t��ֵ��
��3������ת�������Ƿ����������t��ʹ������OB��������OM������OA������ON�е�����������ɵĽǣ�ָ����0���������180��Ľǣ���ƽ���ߣ�������ڣ���ֱ��д��t��ֵ����������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com