
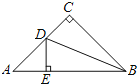
【题目】如图,![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 上的一个动点,
上的一个动点,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() .
.
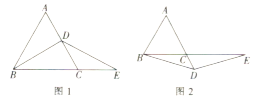
(1)当![]() 是
是![]() 的中点时,求证:
的中点时,求证:![]() .
.
(2)如图1,若点![]() 在边
在边![]() 上,猜想线段
上,猜想线段![]() 与
与![]() 之间的关系,并说明理由.
之间的关系,并说明理由.
(3)如图2,若点![]() 在
在![]() 的延长线上,(1)中的结论是否仍然成立,请说明理由.
的延长线上,(1)中的结论是否仍然成立,请说明理由.
【答案】(1)证明见解析;(2)![]() ,理由见解析;(3)成立,理由见解析.
,理由见解析;(3)成立,理由见解析.
【解析】
(1)根据等边三角形的性质可得![]() ,
,![]() ,然后根据等边对等角可得
,然后根据等边对等角可得![]() ,从而求出
,从而求出![]() ,然后利用等角对等边即可证出
,然后利用等角对等边即可证出![]() ,从而证出结论;
,从而证出结论;
(2)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,根据等边三角形的判定
,根据等边三角形的判定![]() 也是等边三角形,然后利用AAS即可证出
也是等边三角形,然后利用AAS即可证出![]() ,根据全等三角形的性质可得
,根据全等三角形的性质可得![]() ,从而证出结论;
,从而证出结论;
(3)过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,根据等边三角形的判定
,根据等边三角形的判定![]() 也是等边三角形,然后利用AAS即可证出
也是等边三角形,然后利用AAS即可证出![]() ,根据全等三角形的性质可得
,根据全等三角形的性质可得![]() ,从而证出结论;
,从而证出结论;
(1)证明:∵![]() 为等边三角形,
为等边三角形,![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)![]() .
.
理由:如图,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.

∵![]() 是等边三角形,
是等边三角形,
∴![]() 也是等边三角形,
也是等边三角形,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,

∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)如图,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.

∵![]() 是等边三角形,
是等边三角形,
∴![]() 也是等边三角形,
也是等边三角形,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,

∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
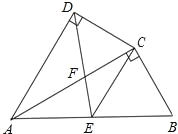
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)求证:△AFD∽△CFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD边AB的中点,连接CE,过点B作BH⊥CE于F,交AC于G,交AD于H.下列说法: ![]() ;②点F是GB的中点;
;②点F是GB的中点; ![]() ;
; ![]() ,其中正确的结论的序号是_____________
,其中正确的结论的序号是_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC 中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F.
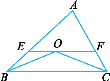
(1)若∠ABC=40°,∠ACB=60°,求∠BOE+∠COF的度数;
(2)若△AEF的周长为8 cm,且BC=4 cm,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+ ![]() 与y轴相交于点A,点B与点O关于点A对称.
与y轴相交于点A,点B与点O关于点A对称.
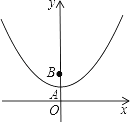
(1)填空:点B的坐标为________;
(2)过点B的直线y=kx+b(其中k<0)与x轴相交于点C,过点C作直线l平行于y轴,P是直线l上一点,且PB=PC,求线段PB的长(用含k的式子表示),并判断点P是否在抛物线上,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,BD平分∠CBA交AC于点D,DE⊥AB于点E,且△DEA的周长为2019cm,则AB=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程对承接了60万平方米的绿化工程,由于情况有变,……,设原计划每天绿化的面积为![]() 万平方米,列方程为
万平方米,列方程为![]() ,根据方程可知省略的部分是( )
,根据方程可知省略的部分是( )
A.实际工作时每天的工作效率比原计划提高了20%,结果提前30天完成了这一任务
B.实际工作时每天的工作效率比原计划提高了20%,结果延误30天完成了这一任务
C.实际工作时每天的工作效率比原计划降低了20%,结果延误30天完成了这一任务
D.实际工作时每天的工作效率比原计划降低了20%,结果提前30天完成了这一任务
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com