
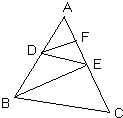
 阅读并填充理由(不完整的补充完整):
阅读并填充理由(不完整的补充完整):| 1 |
| 2 |
| 1 |
| 2 |
 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
 25、下图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD和四边形EFGH都是正方形.
25、下图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD和四边形EFGH都是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 订饭的人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下不完整的统计图:
订饭的人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下不完整的统计图:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
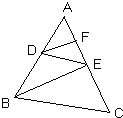 阅读并填充理由(不完整的补充完整):
阅读并填充理由(不完整的补充完整): ________,∠ABE=
________,∠ABE= ________,
________,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com