

分析 (1)过点M作MF⊥BC交BD于点F,推出FM=DN,根据AAS证△EFM和△EDN全等,推出DE=EF,根据正方形的性质和勾股定理求出即可;
(2)过点M作MF⊥BC交BD于点F,推出FM=DN,根据AAS证△EFM和△EDN全等,推出DE=EF,根据正方形的性质和勾股定理求得BD+2DE=$\sqrt{2}$BM,根据已知求出CM的长,证△ABF∽△DNF,得出比例式,代入后求出CD长,即可得到结论.
解答 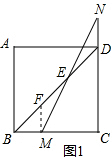 解:(1)如图1,过点M作MF⊥BC交BD于点F,
解:(1)如图1,过点M作MF⊥BC交BD于点F,
∵四边形ABCD是正方形,
∴∠C=90°,
∴FM∥CD,
∴∠NDE=∠MFE,
∴FM=BM,
∵BM=DN,
∴FM=DN,
在△EFM和△EDN中,
$\left\{\begin{array}{l}{∠NDE=∠MFE}\\{∠NED=∠MEF}\\{DN=FM}\end{array}\right.$,
∴△EFM≌△EDN,
∴EF=ED,
∴BD-2DE=BF,
根据勾股定理得:BF=$\sqrt{2}$BM,
即BD-2DE=$\sqrt{2}$BM.
(2)过点M作MH⊥BC交BD于点H,
与(1)证法类似:BD+2DE=BH=$\sqrt{2}$BM,
∴BD=$\sqrt{2}$BC,
∵DE=$\sqrt{2}$,
∴CM=2,
∵AB∥CD,
∴△ABF∽△DNF,
∴AF:FD=AB:ND,
∵AF:FD=1:2,
∴AB:ND=1:2,
∴CD:ND=1:2,
CD:(CD+2)=1:2,
∴CD=2,
∴FD=$\frac{4}{3}$,
∴FD:BM=1:3,
∴DG:BG=1:3,
∴DG=$\frac{\sqrt{2}}{2}$.
点评 本题综合考查了正方形的性质,相似三角形的性质和判定,全等三角形的性质和判定等知识点,此题综合性比较强,难度较大,但题型较好,训练了学生分析问题和解决问题的能力.用的数学思想是类比推理的思想.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y1>y2 | D. | y1<y2<y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
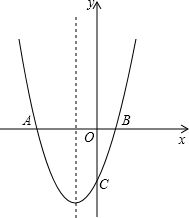 如图,抛物线y=(x+1)2+k 与x轴交于A、B两点,与y轴交于点C(0,-3).
如图,抛物线y=(x+1)2+k 与x轴交于A、B两点,与y轴交于点C(0,-3).查看答案和解析>>
科目:初中数学 来源:2017届四川省遂宁市九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知关于x的方程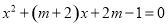 .
.
(1)求证方程有两个不相等的实数根。
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com