
【题目】如图,已知AB=AC,∠A=36°,AB的垂直平分线MD交AC于点D,AB于M,以下结论:①△BCD是等腰三角形;②射线BD是△ACB的角平分线;③△BCD的周长C△BCD=AC+BC;④△ADM≌BCD.正确的有( )
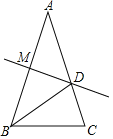
A.①②③B.①②C.①③D.③④
【答案】C
【解析】
①由AB=AC,∠A=36°知∠ABC=∠C=72°,MN是AB的中垂线知AD=BD,∠ABD=∠A=36°,所以∠DBC=36°①正确;②由①和∠ABC=72°,可得∠ABD=36,②错误;③由①知,DA=BD,△BCD的周长=BC+CD+BD=AC+BC=AB+BC,③正确;④由①知∠AMD=90°,而△BCD为锐角三角形,所以④不正确.
由AB=AC,∠A=36°知∠ABC=∠C=72°,
∵MN是AB的中垂线,
∴AD=BD,
∴∠ABD=∠A=36°,
∴∠DBC=36°,
∴①正确,
又∵∠ABC=72°,
∴∠ABD=36°,
∴BD是△ACB的角平分线,
∵三角形的角平分线是线段,②错误,
由AD=BD,AB=AC知,△BCD的周长=BC+CD+BD=AC+BC=AB+BC,
∴③正确,
∵AM⊥MD,而△BCD为锐角三角形,
∴④错误,
∴正确的为:①③.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC中点,F是AC中点,AN是△ABC的外角∠MAC的角平分线,延长DF交AN于点E.
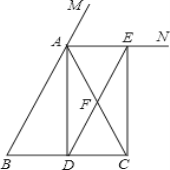
(1)求证:四边形ABDE是平行四边形;
(2)问:线段CE与线段AD有什么关系?请说明你的理由;
(3)当△ABC满足什么条件时,四边形ADCE是一个正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈老师打算购买装扮学校“六一”儿童节活动会场,气球种类有笑脸和爱心两种.两种气球的价格不同,但同一种类的气球价格相同.由于会场布置需要,购买了三束气球(每束![]() 个气球),每束价格如图所示,
个气球),每束价格如图所示,
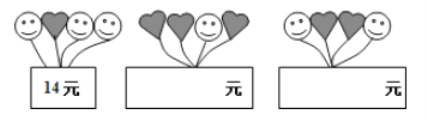
![]() 若笑脸气球的单价是
若笑脸气球的单价是![]() 元,请用含
元,请用含![]() 的整式表示第②束、第③束气球的总价格; (要求结果化简后,填在方框内的相应位置上)
的整式表示第②束、第③束气球的总价格; (要求结果化简后,填在方框内的相应位置上)
![]() 若第②束气球的总价钱比第③束气球的总价钱少
若第②束气球的总价钱比第③束气球的总价钱少![]() 元,求这两种气球的单价.
元,求这两种气球的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
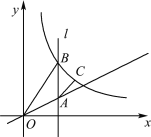
【题目】如图,已知点A是一次函数y=![]() x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=
x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=![]() (x>0)的图象过点B,C,若△OAB的面积为5,则△ABC的面积是________.
(x>0)的图象过点B,C,若△OAB的面积为5,则△ABC的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为![]() .
.
![]()
(问题情境)如图,数轴上点A表示的数为﹣4,点B表示的数为16,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(综合运用)
(1)填空:
①A、B两点间的距离AB= ,线段AB的中点表示的数为 ;
②当t为 秒时,点P与点Q相遇.
(2)①用含t的代数式表示:t秒后,点P表示的数为 ;点Q表示的数为 ;
②若将数轴翻折,使点A与数轴上表示6的点重合,则此时点B与数轴上表示数 的点重合.
(3)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A和B两位同学在化简![]() 时的解答过程如下:
时的解答过程如下:![]()
![]()
A同学:原式=![]() (第一步)
(第一步)
=![]() (第二步)
(第二步)
=![]() (第三步)
(第三步)
B同学:原式=![]() (第一步)
(第一步)
=![]() (第二步)
(第二步)
=![]() (第三步)
(第三步)
(1)请你判断两位同学的解答过程正确吗?
A:_____ ,B:______ (正确的打√,错误的打×)
对于出错的同学,请指出他是从第几步开始出错的?错误的原因是什么?
(2)如果你在(1)中判断两位同学的解答都是错误的,请写出你认为正确的解答过程,否则请跳过此题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某位同学在野营时误入一沼泽地,该同学的体重为500![]() ,其每只鞋的鞋底表面积约为0.02
,其每只鞋的鞋底表面积约为0.02![]() ,而该沼泽地能承受的最大压强为10000Pa(1 Pa =1N / m2)。他若双脚站立,整个身体会陷入该沼泽地吗? ______ (填“会”或“不会”)为什么?_______.如果你认为会陷入,那他在等待救援前该怎么做?_________;如果你认为不会陷入,请跳过此问.
,而该沼泽地能承受的最大压强为10000Pa(1 Pa =1N / m2)。他若双脚站立,整个身体会陷入该沼泽地吗? ______ (填“会”或“不会”)为什么?_______.如果你认为会陷入,那他在等待救援前该怎么做?_________;如果你认为不会陷入,请跳过此问.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究函数![]() 的图象与性质
的图象与性质
(1)函数![]() 的自变量x的取值范围是___;
的自变量x的取值范围是___;
(2)下列四个函数图象中,函数![]() 的图象大致是___;
的图象大致是___;
A.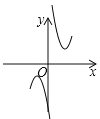 B.
B.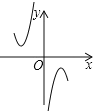 C.
C.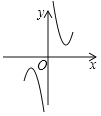 D.
D.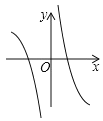
(3)对于函数![]() ,求当
,求当![]() 时,y的取值范围。
时,y的取值范围。
请将下面求解此问题的过程补充完整:
解:∵x>0
∴![]()
=![]()
∵![]()
∴y=____.
(拓展应用)
(4)若函数![]() ,求y的取值范围.
,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知 AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.
(1)证明:△AEF∽△DCE.
(2)若AB=2,AE =3,AD=7,求线段AF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com