
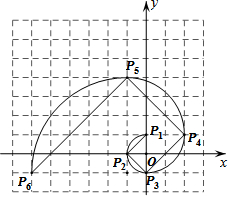
 ���ǰ�1��1��2��3��5��8��13��21������������Ϊ쳲��������У�Ϊ�˽�һ���о���������������Ϊ�뾶��90��Բ��$\widehat{{P_1}{P_2}}$��$\widehat{{P_2}{P_3}}$��$\widehat{{P_3}{P_4}}$�����õ�쳲����������ߣ�Ȼ��˳������P1P2��P2P3��P3P4�����õ��������ߣ���ͼ������֪��P1��0��1����P2��-1��0����P3��0��-1������������ϵĵ�P9������Ϊ��������
���ǰ�1��1��2��3��5��8��13��21������������Ϊ쳲��������У�Ϊ�˽�һ���о���������������Ϊ�뾶��90��Բ��$\widehat{{P_1}{P_2}}$��$\widehat{{P_2}{P_3}}$��$\widehat{{P_3}{P_4}}$�����õ�쳲����������ߣ�Ȼ��˳������P1P2��P2P3��P3P4�����õ��������ߣ���ͼ������֪��P1��0��1����P2��-1��0����P3��0��-1������������ϵĵ�P9������Ϊ��������| A�� | ��-6��24�� | B�� | ��-6��25�� | C�� | ��-5��24�� | D�� | ��-5��25�� |

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
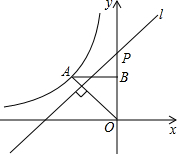 ��ͼ������������y=$\frac{k}{x}$��x��0����ͼ����A��-2��2��������A��AB��y�ᣬ����ΪB����y�����������ȡһ��P��0��t��������P��ֱ��OA�Ĵ���l����ֱ��lΪ�Գ��ᣬ��B����ԳƱ任�õ��ĵ�B���ڴ˷�����������ͼ���ϣ���t��ֵ��1+$\sqrt{5}$��
��ͼ������������y=$\frac{k}{x}$��x��0����ͼ����A��-2��2��������A��AB��y�ᣬ����ΪB����y�����������ȡһ��P��0��t��������P��ֱ��OA�Ĵ���l����ֱ��lΪ�Գ��ᣬ��B����ԳƱ任�õ��ĵ�B���ڴ˷�����������ͼ���ϣ���t��ֵ��1+$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
| A�� | ac��0 | B�� | ��x��1ʱ��y��ֵ��x���������С | ||
| C�� | 3�Ƿ���ax2+��b-1��x+c=0��һ���� | D�� | ��-1��x��3ʱ��ax2+��b-1��x+c��0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
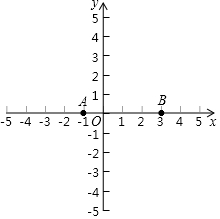 ��ͼ����ƽ��ֱ������ϵxOy�У�������y=-x2+bx+c����A��-1��0����B��3��0�����㣮
��ͼ����ƽ��ֱ������ϵxOy�У�������y=-x2+bx+c����A��-1��0����B��3��0�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
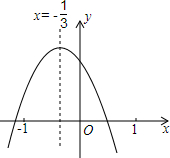 ���ִ���ͼ��ʾ�Ķ��κ���y=ax2+bx+c��a��0����ͼ���У��۲�ó�������4����Ϣ��
���ִ���ͼ��ʾ�Ķ��κ���y=ax2+bx+c��a��0����ͼ���У��۲�ó�������4����Ϣ��| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com