
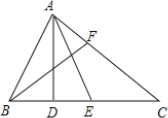
【题目】已知AD⊥BC,BE=CE,∠ABC=2∠C,BF为∠B的平分线.求证:AB=2DE.
科目:初中数学 来源: 题型:
【题目】为早日实现脱贫奔小康的宏伟目标,我市结合本地丰富的山水资源,大力发展旅游业,王家庄在当地政府的支持下,办起了民宿合作社,专门接待游客,合作社共有80间客房.根据合作社提供的房间单价x(元)和游客居住房间数y(间)的信息,乐乐绘制出y与x的函数图象如图所示:
(1)求y与x之间的函数关系式;
(2)合作社规定每个房间价格不低于60元且不超过150元,对于游客所居住的每个房间,合作社每天需支出20元的各种费用,房价定为多少时,合作社每天获利最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
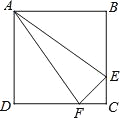
A. 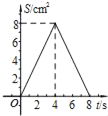 B.
B. 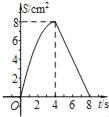
C. 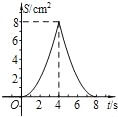 D.
D. 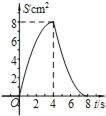
查看答案和解析>>
科目:初中数学 来源: 题型:
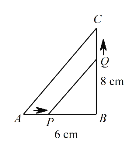
【题目】如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿AB边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动).
(1)如果P,Q分别从A,B两点同时出发,经过几秒钟,△PBQ的面积等于△ABC面积的三分之一?
(2)如果P,Q两点分别从A,B两点同时出发,几秒钟后,P,Q相距6厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
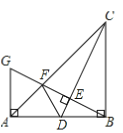
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D是线段AB上的一点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:①![]() ②若点D是AB的中点,则AF=
②若点D是AB的中点,则AF=![]() AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若
AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若![]() ,则
,则![]() ,其中正确的结论序号是( )
,其中正确的结论序号是( )
A. ①② B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晓东在解一元二次方程时,发现有这样一种解法:如:解方程x(x+4)=6.
解:原方程可变形,得[(x+2)﹣2][(x+2)+2]=6.(x+2)2﹣22=6,(x+2)2=6+22,(x+2)2=10.直接开平方并整理,得![]() ,
,![]() .我们称晓东这种解法为“平均数法”.
.我们称晓东这种解法为“平均数法”.
(1)下面是晓东用“平均数法”解方程(x+2)(x+6)=5时写的解题过程.
解:原方程可变形,得
[(x+□)﹣〇][(x+□)+〇]=5.
(x+□)2﹣〇2=5,
(x+□)2=5+〇2.
直接开平方并整理,得x1=☆,x2=¤.
上述过程中的“□”,“〇”,“☆”,“¤”表示的数分别为 , , , .
(2)请用“平均数法”解方程:(x﹣3)(x+1)=5.
查看答案和解析>>
科目:初中数学 来源: 题型:
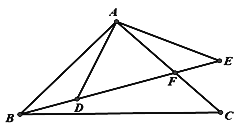
【题目】如图,点B、D、E在一条直线上,BE与AC相交于点F,且![]()
⑴求证:△ABC∽△ADE;
⑵求证:∠BAD=∠CAE;
⑶若∠BAD=18°,求∠EBC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com