
分析 (1)设第一次的进价为x元,则第二次进价为(1+20%)x元,根据题意可得:第二次所进干果数量-第一次的数量=450千克,根据等量关系列出方程,再解即可‘
(2)首先计算出第二次的干果数量,再用每千克的利润×总量可得总利润.
解答 解:(1)设第一次的进价为x元,由题意得:
$\frac{9000}{(1+20%)x}$-$\frac{3000}{x}$=450,
解得:x=10,
经检验:x=10是原分式方程的解,
答:该种干果的第一次进价是每千克10元;
(2)第二批进的干果数量:9000÷[(1+20%)×10]=750(千克),
[16-(1+20%)×10]×750=3000(元),
答:超市可以盈利3000元.
点评 此题主要考查了分式方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:填空题
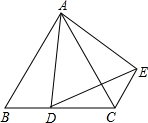 如图所示,△ABC是等边三角形,点D在BC上,△ABD经过逆时针方向旋转后到达△ACE的位置;
如图所示,△ABC是等边三角形,点D在BC上,△ABD经过逆时针方向旋转后到达△ACE的位置;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 123.88×108 | B. | 1.2388×1010 | C. | 1.2×1010 | D. | 0.12388×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 型号 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 销售量(双) | 4 | 6 | 11 | 17 | 8 | 5 | 3 |
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com