
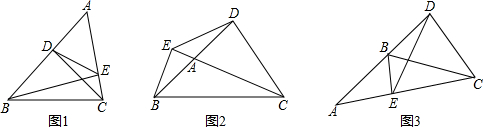
分析 (1)证出△ADC∽△AEB,求出$\frac{AD}{AC}=\frac{AE}{AB}$,再求出△ADE∽△ACB即可;
(2)①在BE上截取BH=EC,求出∠1=∠2,BD=DC,根据SAS推出△BDH≌△CDE,根据全等得出DH=DE,∠3=∠4,求出△DHE为等腰直角三角形,推出BE-EC=BE-BH=HE=$\sqrt{2}$DE即可;②原结论不成立,结论应为:EC-BE=$\sqrt{2}$DE;
(3)延长EB到H,使BH=EC,证△ADC∽△ABE,△ADE∽△ABC,求出△DBC为等腰直角三角形,根据SAS推出△BDH≌△CDE,根据全等得出DE=DH,求出△EDH为等腰直角三角形,推出EC+BE=$\sqrt{2}$DE,设BE=x,求出EC=4-x,在Rt△EBC中,由勾股定理得${x^2}+{({4-x})^2}={({\sqrt{10}})^2}$,求出x,解直角三角形求出tan∠3=$\frac{BE}{EC}=\frac{1}{3}$,延长DE,过点A作AF⊥DE的延长线于点F,在Rt△AFD中,tan∠4=tan∠3=$\frac{1}{3}$,设AF=EF=a 则DF=3a,求出DE=3a-a=2a=$2\sqrt{2}$,即可求出答案.
解答 (1)解:如图1:∵CD⊥AB,BE⊥AC,垂足分别是D、E,
∴∠AEB=∠ADC=90°
∵∠A=∠A
∴△ADC∽△AEB
∴$\frac{AD}{AE}=\frac{AC}{AB}$
∴$\frac{AD}{AC}=\frac{AE}{AB}$,
又∵∠A=∠A,
∴△ADE∽△ACB
∴∠AED=∠ABC=45°;
(2)①证明:如图2:在BE上截取BH=EC.
∵△ADC∽△ABE,
∴∠1=∠2,
∵CD⊥AB,
∴∠BDC=90°
∵∠ABC=45°,
∴BD=DC,
在△BDH和△CDE中
$\left\{\begin{array}{l}{BD=DC}\\{∠1=∠2}\\{BH=CE}\end{array}\right.$
∴△BDH≌△CDE(SAS),
∴DH=DE,∠3=∠4,
∵∠3+∠5=90°,
∴∠HDE=∠4+∠5=90°,
∴△DHE为等腰直角三角形,
∴BE-EC=BE-BH=HE=$\sqrt{2}$DE,
∴BE-EC=$\sqrt{2}$DE;
②如图3,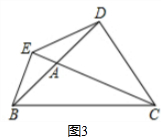
原结论不成立,结论应为:EC-BE=$\sqrt{2}$DE;
(3)如图4:延长EB到H,使BH=EC,
同理可证:△ADC∽△ABE,△ADE∽△ABC,
∠DEC=45°,
∴△DBC为等腰直角三角形,
∵∠1=∠2=∠DCE,
在△BDH和△CDE中
$\left\{\begin{array}{l}{BD=DC}\\{∠2=∠DCE}\\{BH=CE}\end{array}\right.$
∴△BDH≌△CDE(SAS),
∴DE=DH,
∴∠5=180°-90°-45°=45°,
∴∠5=∠H=45°,
∴△EDH为等腰直角三角形,
∴HB+BE=EC+BE=HB=$\sqrt{2}$DE
∴EC+BE=$\sqrt{2}$DE,
设BE=x
∵△DBC为等腰直角三角形
∴BC=$\sqrt{2}$DC=$\sqrt{10}$,
∵EC+BE=$\sqrt{2}$DE,
即EC+x=$\sqrt{2}$•$2\sqrt{2}$=4,
∴EC=4-x,
在Rt△EBC中,由勾股定理得:${x^2}+{({4-x})^2}={({\sqrt{10}})^2}$,
解得:x=1或3,
∵0<BE<2,
∴BE=1,
∴tan∠3=$\frac{BE}{EC}=\frac{1}{3}$,
延长DE,过点A作AF⊥DE的延长线于点F,
在Rt△AFD中,tan∠4=tan∠3=$\frac{1}{3}$,
∵∠AEF=∠DEC=45°,
∴设AF=EF=a 则DF=3a,
∴DE=3a-a=2a=$2\sqrt{2}$,
∴a=$\sqrt{2}$,
∴AE=$\sqrt{2}$•$\sqrt{2}$=2.
点评 本题考查了全等三角形的性质和判定,勾股定理,解直角三角形,等腰直角三角形的性质等知识点的应用,能综合运用性质进行推理是解此题的关键,综合性比较强,难度偏大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
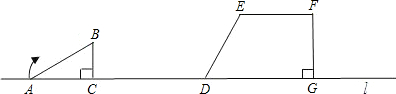
 王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(1,-2),你能帮她求出其他各景点的坐标吗?
王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示.可是她忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(1,-2),你能帮她求出其他各景点的坐标吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,E(2,3),F(3,2)在正方形OABC的边上,⊙D分别切OE,OF于E,F,则⊙D的半径为$\frac{{\sqrt{13}}}{5}$.
如图,E(2,3),F(3,2)在正方形OABC的边上,⊙D分别切OE,OF于E,F,则⊙D的半径为$\frac{{\sqrt{13}}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
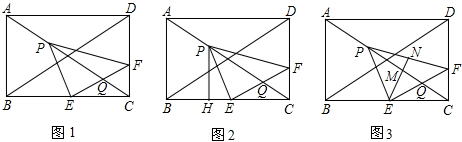
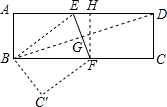 如图,矩形ABCD的长AD=9cm,宽AB=3cm,将它折叠,使点D与点B重合,求折叠后DE的长和EF的长分别是( )
如图,矩形ABCD的长AD=9cm,宽AB=3cm,将它折叠,使点D与点B重合,求折叠后DE的长和EF的长分别是( )| A. | 5cm,3cm | B. | 5cm,$\sqrt{10}$cm | C. | 6cm,$\sqrt{10}$cm | D. | 5cm,4cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
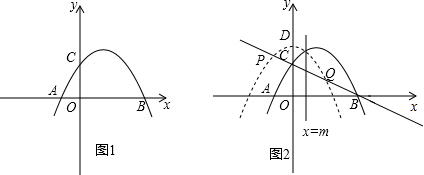
 如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,-1),并且与y轴交于点C(0,3),与x轴交于两点A,B.
如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,-1),并且与y轴交于点C(0,3),与x轴交于两点A,B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com