
如图,在等边三角形
ABC中,P是BC上的任意一点,线段AP的垂直平分线分别交AB、AC于点M、N.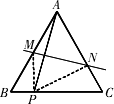
求证:
BP·CP=BM·CN.|
分析:要证明 BP·CP=BM·CN,即证明证明:连接 PM、PN.因为 MN是AP的垂直平分线,所以MA=MP,NA=NP.所以∠ MPA=∠MAP,∠NPA=∠NAP.所以∠ MPN=∠MPA+∠NPA=∠MAP+∠NAP=∠MAN=60°.所以∠ BPM+∠CPN=180°-∠MPN=120°.因为∠ BPM+∠BMP=180°-∠B=120°,所以∠BMP=∠CPN.又因为∠ B=∠C=60°,所以△BPM∽△CNP.所以 点评:在题设的图形中没有明显的三角形相似的情况下,我们可以顺着要证明的比例线段中的字母,利用辅助线构造出三角形,再利用已知条件证明构造出来的三角形相似. |


科目:初中数学 来源: 题型:
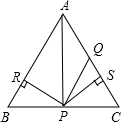 如图,在等边三角形△ABC中,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,且PR=PS,下面给出的四个结论:①点P在∠A的平分线上,②AS=AR,③QP∥AR,④△BRP≌△QSP,则其中正确的是( )
如图,在等边三角形△ABC中,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,且PR=PS,下面给出的四个结论:①点P在∠A的平分线上,②AS=AR,③QP∥AR,④△BRP≌△QSP,则其中正确的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com