
【题目】如图,P、G是菱形ABCD的边BC、DC的中点,K是菱形的对角线BD上的动点,若BD=8,AC=6,则KP+KG的最小值是_____.

科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
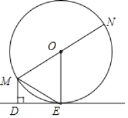
【题目】已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.
求证:(1)DE是⊙O的切线;
(2)ME2=MDMN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,三角形三个内角平分线的交点叫做三角形的内心,已知点I为△ABC的内心.
(1)如图1,连接AI并延长交BC于点D,若AB=AC=3,BC=2,求ID的长;
(2)如图2,过点I作直线交AB于点M,交AC于点N.
①若MN⊥AI,求证:MI2=BMCN;
②如图3,AI交BC于点D,若∠BAC=60°,AI=4,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,反比例函数![]() (
(![]() >0)图象上一点A,连结OA,作AB丄
>0)图象上一点A,连结OA,作AB丄![]() 轴于点B,作BC∥OA交反比例函数图象于点C,作CD丄
轴于点B,作BC∥OA交反比例函数图象于点C,作CD丄![]() 轴于点D,若点A、点C横坐标分别为m、n,则m:n的值为_______________.
轴于点D,若点A、点C横坐标分别为m、n,则m:n的值为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:
①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点P在AB边上(不含端点A,B),以PC为直径作圆.圆与BC,CA分别相交于点M,N,则线段MN长度的最小值为________.
,动点P在AB边上(不含端点A,B),以PC为直径作圆.圆与BC,CA分别相交于点M,N,则线段MN长度的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2.
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:

(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com