
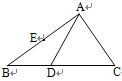
【题目】如图,△ABC中,D为BC边上的点,∠CAD=∠CDA,E为AB边的中点.
(1)尺规作图:作∠C的平分线CF,交AD于点F(保留作图痕迹,不写作法);
(2)连结EF,EF与BC是什么位置关系?为什么?
(3)若四边形BDFE的面积为9,求△ABD的面积.
【答案】(1)作图见解析;
(2)EF∥BC,原因见解析;
(3)△ABD的面积为12
【解析】(本小题满分12分)
解:(1)尺规作图略;…………………………………………………………3分
(2)EF∥BC(即EF平行于BC).……………………………………1分
原因如下:如图1,∵∠CAD=∠CDA,
∴AC=DC(等角对等边),即△CAD为等腰三角形;…………………2分
又CF是顶角∠ACD的平分线,由“三线合一”定理,
知CF是底边AD的中线,即F为AD的中点,……………………………3分
结合E是AB的中点,得EF为△ABD的中位线,………………………4分
∴EF∥BD,从而EF∥BC;……………………………………………5分
(3)由(2)知EF∥BC,∴△AEF∽△ABD,…………………1分
∴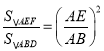 ,……………………………………………………………2分
,……………………………………………………………2分
又∵AE=![]() AB,∴得
AB,∴得![]() ,
,
把S四边形BDFE=9代入其中,解得
S△AEF=3,………………………………………………………………………3分
∴S△ABD=S△AEF+S四边形BDFE=3+9=12,……………………………4分
即△ABD的面积为12.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的面积为acm2 , 对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,连接AC1交BD于O1 , 以AB、AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AOn﹣1CnB的面积为( )cm2 . 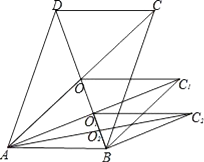
A.![]() a
a![]()
B.![]() a
a![]()
C.![]() a
a![]()
D.![]() a
a![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
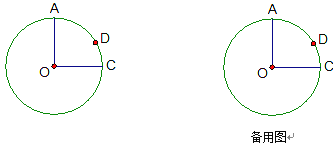
【题目】如图,⊙O的半径OA⊥OC,点D在![]() 上,且
上,且![]() =2
=2![]() ,OA=4.
,OA=4.
(1)∠COD= °;
(2)求弦AD的长;
(3)P是半径OC上一动点,连结AP、PD,请求出AP+PD的最小值,并说明理由.
(解答上面各题时,请按题意,自行补足图形)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() =
=![]() +
+![]() +
+![]() 的顶点M是直线
的顶点M是直线![]() =-
=-![]() 和直线
和直线![]() =
=![]() +
+![]() 的交点.
的交点.
(1)若直线![]() =
=![]() +
+![]() 过点D(0,-3),求M点的坐标及二次函数
过点D(0,-3),求M点的坐标及二次函数![]() =
=![]() +
+![]() +
+![]() 的解析式;
的解析式;
(2)试证明无论![]() 取任何值,二次函数
取任何值,二次函数![]() =
=![]() +
+![]() +
+![]() 的图象与直线
的图象与直线![]() =
=![]() +
+![]() 总有两个不同的交点;
总有两个不同的交点;
(3)在(1)的条件下,若二次函数![]() =
=![]() +
+![]() +
+![]() 的图象与
的图象与![]() 轴交于点C,与
轴交于点C,与![]() 的右交点为A,试在直线
的右交点为A,试在直线![]() =-
=-![]() 上求异于M的点P,使P在△CMA的外接圆上.
上求异于M的点P,使P在△CMA的外接圆上.
查看答案和解析>>
科目:初中数学 来源: 题型:
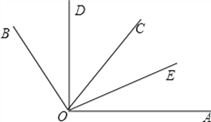
【题目】如图,OD平分∠BOC,OE平分∠AOC.若∠BOC=70°,∠AOC=50°.
(1)求出∠AOB及其补角的度数;
(2)请求出∠DOC和∠AOE的度数,并判断∠DOE与∠AOB是否互补,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种数字化的信息传输中,先将信息转化为由数字 ![]() 和
和 ![]() 组成的数字串,并对数字串进行加密后再传输.现采用一种简单的加密方法:将原有的每个
组成的数字串,并对数字串进行加密后再传输.现采用一种简单的加密方法:将原有的每个 ![]() 都变成
都变成 ![]() ,原有的每个
,原有的每个 ![]() 都变成
都变成 ![]() .我们用
.我们用 ![]() 表示没有经过加密的数字串.这样对
表示没有经过加密的数字串.这样对 ![]() 进行一次加密就得到一个新的数字串
进行一次加密就得到一个新的数字串 ![]() ,对
,对 ![]() 再进行一次加密又得到一个新的数字串
再进行一次加密又得到一个新的数字串 ![]() ,依此类推,
,依此类推, ![]() .例如
.例如 ![]() :
: ![]() ,则
,则 ![]() :
: ![]() .若已知
.若已知 ![]() :
: ![]() ,则
,则 ![]() ________________;若数字串
________________;若数字串 ![]() 共有
共有 ![]() 个数字,则数字串
个数字,则数字串 ![]() 中相邻两个数字相等的数对至少有________________对.
中相邻两个数字相等的数对至少有________________对.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com