练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    2014年世界杯足球赛6月12日-7月13日在巴西举行，某初中学校为了了解本校2400名学生对此次世界杯的关注程度，以便做好引导和教育工作，随机抽取了200名学生进行调查，按年级人数和关注程度，分别绘成了条形统计图(图1)和扇形统计图(图2》.

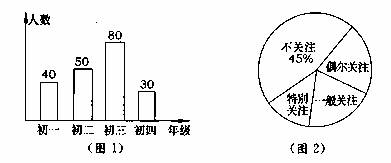
       (1)四个年级被调查人数的中位数是多少?

        (2)如果把‘特别关住“一般关注“偶尔关注.都统计成关注，那么全校关注本届世界杯

    的学生大约有多少名宁

    (3)在这次调查中，初四年级共有甲、乙、丙、丁四人..特别关注，本届世界杯，现准备从四人中随机抽取两人进行座谈，请用列表法或画树状田的方法求出抽取的两人恰好是甲和乙的概率，



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


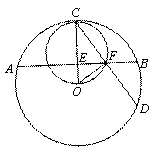
    如图，在⊙O中，半径OC与弦AB垂直，垂足为E，以OC为直径的圆与弦AB的一个交点为F，D是CF延长线与⊙O的交点，若OE=4，OF=6，求⊙O的半径和CD的长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    小明放学后步行回家，他离家的路程米与步行时间分钟的函数图象如图所示，则他步行回家的平均速度是        米/分钟．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    关于x的方程的两根的平方和是5"则a的值是

    A，一1或5  B 1    C    5     D-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在一个不透明的袋子中装有若干个除颜色外形状大小完全相同的球，如果其中有3个

    白球，且摸出白球的概率是1/4，那么袋子中共有球_个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


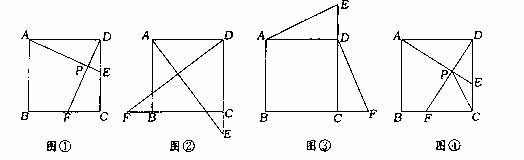
    在正方形ABCD中，动点E.F分别从D.C两点同时出发，以相同的速度在直线DC.CB上移动，

    (1)如图①，当点E自D向C,点F自C向B移动时。连接AE和DF交于点P,请你写出AE与DF的关系，井说明理由:

    (2)如图②，当E.F分别移动到边DC. CB的延长线上时。连接AE和DF,(1)中的结论还成立么?(请你直接回答“是’，或“否”，不须证明)

    (3)如图③、当E,F分别在边CD. BC的延长线上移动时.连接AE和DF.(1〕中的结论还成立吗?请说明理由；

    (4)如图④，当E.F分别在边DC. CB上移动时，连接AE和DF,交于点P.由于点E.F的移动，使得点P也随之运动.请你画出点P运动路径的草图_若AD-2,试求出线段CP的最小值

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    菱形的两条对角线长分别是6和8，则此菱形的边长是

    A. 10             B. 8               C. 6              D. 5

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点A，B分别在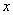轴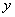，轴上，点D在第一象限内，DC⊥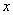轴于点C，AO=CD=2，AB=DA=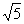，反比例函数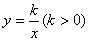的图象过CD的中点E。

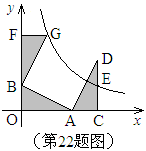    （1）求证：△AOB≌△DCA；

    （2）求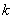的值；

    （3）△BFG和△DCA关于某点成中心对称，其中点F在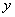轴上，试判断点G是否在反比例函数的图象上，并说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，直线AB，CD被BC所截，若AB∥CD，∠1=45°，∠2=35°，则∠3=     度

    查看答案和解析>>

    同步练习册答案