
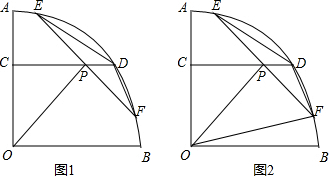
分析 (1)连接OE,首先求出OP的长,在Rt△OPE中,求出EP,根据垂径定理EF=2EP即可解决问题.
(2)首先判断∠EOP=30°,求出EP,结合AC=2求出OC,在Rt△OCP中,可求出CP的长.
(3)如图3中,连接OE、OD,作DH⊥EF于H.由△COP∽△HPD,得$\frac{OP}{DP}$=$\frac{PC}{DH}$,求出DH,再根据y=$\frac{{S}_{△DEF}}{{S}_{△OEF}}$=$\frac{\frac{1}{2}•EF•DH}{\frac{1}{2}•EF•OP}$,计算即可.
解答 解:(1)如图1中,连接OE.
∵OC=CP=3,∠OCP=90°,
∴OP=3$\sqrt{3}$,
∵OP⊥EF,
∴EP=PF,EF=2EP,
在Rt△OPE中,∵∠OPE=90°,OE=5,OP=3$\sqrt{2}$,
∴EP=$\sqrt{O{E}^{2}-O{P}^{2}}$=$\sqrt{25-18}$=$\sqrt{7}$,
∴EF=2$\sqrt{7}$.
(2)如图2中,连接OE.
∵OE=OF,∠EOF=60°,
∴△EOF是等边三角形,
∵OP⊥EF,
∴∠EOP=∠FOP=30°,
∴OP=OE•cos30°=$\frac{5\sqrt{3}}{2}$,
在Rt△COP中,PC=$\sqrt{O{P}^{2}-O{C}^{2}}$=$\frac{\sqrt{39}}{2}$.
(3)如图3中,连接OE、OD,作DH⊥EF于H.
在Rt△COD中,CD=$\sqrt{O{D}^{2}-O{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴DP=4-x,OP=$\sqrt{O{C}^{2}+C{P}^{2}}$=$\sqrt{9+{x}^{2}}$,
∵∠CPO+∠DPH=90°,∠COP+∠CPO=90°,
∴∠COP=∠DPH,∵∠OCP=∠DHP=90°,
∴△COP∽△HPD,
∴$\frac{OP}{DP}$=$\frac{PC}{DH}$,
∴$\frac{\sqrt{9+{x}^{2}}}{4-x}$=$\frac{x}{DH}$,
∴DH=$\frac{x(4-x)}{\sqrt{9+{x}^{2}}}$,
∴y=$\frac{{S}_{△DEF}}{{S}_{△OEF}}$=$\frac{\frac{1}{2}•EF•DH}{\frac{1}{2}•EF•OP}$=$\frac{4x-{x}^{2}}{9+{x}^{2}}$.($\sqrt{6}$≤x<4).
点评 此题考查了圆的综合,涉及了垂径定理、勾股定理、相似三角形的判定与性质,综合考察的知识点较多,解答本题关键还是基本知识的掌握,要求同学们会运用数形结合思想解题.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:选择题
| A. | 1.643×103立方米 | B. | 0.2643×108立方米 | ||
| C. | 26.43×106立方米 | D. | 2.643×107立方米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
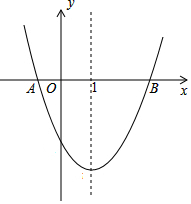 如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点、点A在点B的左侧,它的顶点D(1,-4).
如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点、点A在点B的左侧,它的顶点D(1,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某宾馆在重新装修后,考虑在大厅内的主楼梯上铺设地毯,已知主楼梯宽3米,其剖面如图所示,请你计算一下:
某宾馆在重新装修后,考虑在大厅内的主楼梯上铺设地毯,已知主楼梯宽3米,其剖面如图所示,请你计算一下:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com