
【题目】已知△ABC中,BE平分∠ABC,点P在射线BE上.

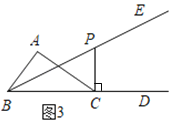
(1)如图1,若∠ABC=40°,CP∥AB,求∠BPC的度数;
(2)如图2,若∠BAC=100°,∠PBC=∠PCA,求∠BPC的度数;
(3)若∠ABC=40°,∠ACB=30°,直线CP与△ABC的一条边垂直,画出相应图形并求∠BPC的度数.
【答案】(1)∠BPC=20°;(2)∠BPC=100°;(3)画出相应图形见解析;∠BPC的度数为70°或40°或110°.
【解析】
(1)根据角平分线的定义与平行线的性质,即可求解;
(2)根据三角形内角和定理,可得∠A=∠BPC,进而即可求解;
(3)分3种情况:①当CP⊥BC时,②当CP⊥AC时, ③当CP⊥AB时,分别画出图形,即可求解.
(1)∵BE平分∠ABC,∠ABC=40°,
∴∠ABP=![]() =20°,
=20°,
∵CP∥AB,
∴∠BPC=∠ABP=20°;
(2)∵BE平分∠ABC,∠PBC=∠PCA
∴∠ABP=∠PBC=∠PCA
△ABO中,∠A+∠ABP+∠AOB=180°,
△PCO中,∠BPC+∠PCA+∠POC=180°,
∵∠ABP=∠PCA, ∠AOB=∠POC
∴∠A=∠BPC =100°
即∠BPC=100°;
(3)①当CP⊥BC时,如图3,则∠BCP=90°,
∵∠PBC=20°,
∴∠BPC=70°;
②当CP⊥AC时,如图4,则∠ACP=90°,
△BCP中,∠BPC=180°﹣20°﹣30°﹣90°=40°;
③当CP⊥AB时,延长CP交直线AB于G,如图5,则∠BGC=90°,
∵∠ABC=40°,
∴∠BCG=50°
△BPC中,∠BPC=180°﹣50°﹣20°=110°;
综上,∠BPC的度数为70°或40°或110°.


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】请观察如下算式,并解答问题:
15×35; 16×34; 17×33; 18×32; 19×31.
(1)请根据上述算式规律写下去,其乘积的最大值是_______.
(2)设“a2﹣b2=15×35”试求a,b并将其余算式写成两数字平方差的形式;
(3)试由(1)、(2)猜测一个一般性的结论.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形![]() 中,
中, ![]() ,垂足为
,垂足为![]() 与
与![]() 的延长线相交于
的延长线相交于![]() ,且
,且![]() ,连接
,连接![]() ;
;
(1)如图![]() ,求证:四边形
,求证:四边形![]() 是菱形;
是菱形;
(2)如图![]() ,连接
,连接![]() ,若
,若![]() ,在不添加任何辅助线的情况下,直接写出图
,在不添加任何辅助线的情况下,直接写出图![]() 中所有面积等于
中所有面积等于![]() 的面积的钝角三角形.
的面积的钝角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y= ![]() 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=
在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y= ![]() 在第一象限内的图象交于点P,且△POA的面积为2.
在第一象限内的图象交于点P,且△POA的面积为2.
(1)求k的值.
(2)求平移后的直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)操作发现:
如图①,在正方形ABCD中,过A点有直线AP,点B关于AP的对称点为E,连接DE交AP于点F,当∠BAP=20°时,则∠AFD=°;当∠BAP=α°(0<α<45°)时,则∠AFD=;猜想线段DF,EF,AF之间的数量关系:DF﹣EF=AF(填系数);
(2)数学思考:
如图②,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=120°”,其他条件不变,则∠AFD=;线段DF,EF,AF之间的数量关系是否发生改变,若发生改变,请写出数量关系并说明理由;
(3)类比探究:
如图③,若将“正方形ABCD中”改成“菱形ABCD中,∠BAD=α°”,其他条件不变,则∠AFD=°;请直接写出线段DF,EF,AF之间的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α
(1)用含α的式子表示h(不必指出α的取值范围);
(2)用含α的式子表示h(不必指出α的取值范围);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司4月份销售某厂汽车,在一定范围内,每辆汽车的进价与销售量有如下关系:若当月仅售出1辆汽车,则该汽车的进价为30万元,每多售出1辆,所有售出汽车的进价均降低0.1万元/辆,月底厂家一次性返利给销售公司,每辆返利0.5万元.
(1)若该公司当月售出5辆汽车,则每辆汽车的进价为 万元.
(2)若汽车的售价为31万/辆,该公司计划当月盈利12万元,那么需要售出多少辆汽车?(盈利=销售利润+返利)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,四边形OABC为矩形,OA在x轴正半轴上,OC在y轴正半轴上,且A(10,0)、C(0,8)
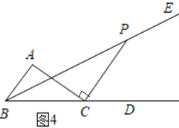
(1)如图1,在矩形OABC的边AB上取一点E,连接OE,将△AOE沿OE折叠,使点A恰好落在BC边上的F处,求AE的长;
(2)将矩形OABC的AB边沿x轴负方向平移至MN(其它边保持不变),M、N分别在边OA、CB上且满足CN=OM=OC=MN.如图2,P、Q分别为OM、MN上一点.若∠PCQ=45°,求证:PQ=OP+NQ;
(3)如图3,S、G、R、H分别为OC、OM、MN、NC上一点,SR、HG交于点D.若∠SDG=135°,HG=4![]() ,求RS的长.
,求RS的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com