

分析 (1)结论:∠COD=90°,只要证明∠OCD+∠ODC=90°即可解决问题.
(2)由RT△AOC∽RT△BDO,得$\frac{AC}{BO}$=$\frac{AO}{BD}$,由此即可解决问题.
(3)分两种情形①如图②中,当△PQD∽△ACO时,②如图②中,当△PQD∽△AOC时,分别计算即可.
解答 解:(1)∠COD=90°.
理由:如图①中,∵AB是直径,AM、BN是切线,
∴AM⊥AB,BN⊥AB,
∴AM∥BN,
∵CA、CP是切线,
∴∠ACO=∠OCP,同理∠ODP=∠ODB,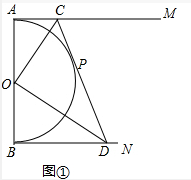
∵∠ACD+∠BDC=180°,
∴2∠OCD+2∠ODC=180°,
∴∠OCD+∠ODC=90°,
∴∠COD=90°.
(2)如图①中,∵AB是直径,AM、BN是切线,
∴∠A=∠B=90°,
∴∠ACO+∠AOC=90°,
∵∠COD=90°,
∴∠BOD+∠AOC=90°,
∴∠ACO=∠BOD,
∴RT△AOC∽RT△BDO,
∴$\frac{AC}{BO}$=$\frac{AO}{BD}$,
即AC•BD=AO•BO,
∵AB=6,
∴AO=BO=3,
∴AC•BD=9.
(3)△PQD能与△ACO相似.
∵CA、CP是⊙O切线,
∴AC=CP,∠1=∠2,
∵DB、DP是⊙O切线,
∴DB=DP,∠B=∠OPD=90°,OD=OD,
∴RT△ODB≌RT△ODP,
∴∠3=∠4,
①如图②中,当△PQD∽△ACO时,∠5=∠1,
∵∠ACO=∠BOD,即∠1=∠3,
∴∠5=∠4,
∴DQ=DO,
∴∠PDO=∠PDQ,
∴△DCQ≌△DCO,
∴∠DCQ=∠2,
∵∠1+∠2+∠DCQ=180°,
∴∠1=60°=∠3,
在RT△ACO,RT△BDO中,分别求得AC=$\sqrt{3}$,BD=3$\sqrt{3}$,
∴AC:BD=1:3.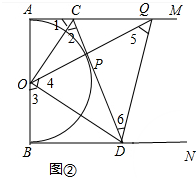
②如图②中,当△PQD∽△AOC时,∠6=∠1,
∵∠2=∠1,
∴∠6=∠2,
∴CO∥QD,
∴∠1=∠CQD,
∴∠6=∠CQD,
∴CQ=CD,
∵S△CDQ=$\frac{1}{2}$•CD•PQ=$\frac{1}{2}$•CQ•AB,
∴PQ=AB=6,
∵CO∥QD,
∴$\frac{PC}{PD}$=$\frac{PO}{PQ}$,即$\frac{AC}{BD}$=$\frac{3}{6}$,
∴AC:BD=1:2
点评 本题考查圆的综合题、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是灵活掌握这些知识的应用,学会分类讨论,注意不能漏解,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | m-2>n-2 | B. | $\frac{m}{2}$>$\frac{n}{2}$ | C. | m2>n2 | D. | 2m+1>2n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}×\sqrt{\frac{1}{2}}=1$ | B. | $\sqrt{{{({-5})}^2}}=-5$ | C. | $\sqrt{6}÷\sqrt{3}=2$ | D. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将一张边长为4的正三角形纸片剪成四个全等的小正三角形,得到4个小正三角形,然后将其中的一个三角形再剪成四个全等的小正三角形,得到7个小正三角形.根据以上操作,若得到2017个小正三角形时,则最小正三角形的面积等于( )
如图,将一张边长为4的正三角形纸片剪成四个全等的小正三角形,得到4个小正三角形,然后将其中的一个三角形再剪成四个全等的小正三角形,得到7个小正三角形.根据以上操作,若得到2017个小正三角形时,则最小正三角形的面积等于( )| A. | $\frac{\sqrt{3}}{{4}^{670}}$ | B. | ($\frac{1}{4}$)671$•\sqrt{3}$ | C. | $\frac{1}{{4}^{671}}$ | D. | $\frac{2\sqrt{3}}{{4}^{670}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
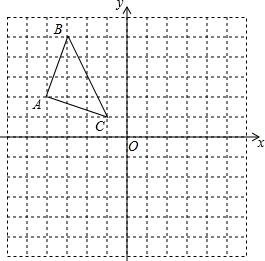 已知:如图,已知△ABC
已知:如图,已知△ABC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com