

分析 (1)设∠ABF=x,则∠FBC=90°-x,根据三角形的内角和表示∠BCF=$\frac{1}{2}$x+45°,则∠BFC=∠BCF,得BF=BC,根据正方形的性质得:AB=BF,从而可得:∠FAB=∠BFA;
(2)如图,延长FG交AB的延长线于M,作BK⊥AF于K,AH⊥BF于H.设AB=BF=x.想办法用x不是AH,由△ABH∽△BCF,可得$\frac{AB}{BE}$=$\frac{AH}{BC}$,列出方程即可解决问题;
解答 证明:(1)设∠ABF=x,则∠FBC=90°-x,
∵∠BFC=$\frac{1}{2}$∠ABF+45°=$\frac{1}{2}$x+45°,
∴∠BCF=180°-(90°-x)-($\frac{1}{2}$x+45°)=$\frac{1}{2}$x+45°,
∴∠BFC=∠BCF,
∴BF=BC,
∵四边形ABCD是正方形,
∴AB=BC,
∴AB=BF,
∴∠FAB=∠BFA;
(2)如图,延长FG交AB的延长线于M,作BK⊥AF于K,AH⊥BF于H.设AB=BF=x.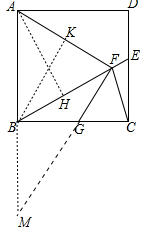
∵BA=BF,
∴∠BAF=∠BFA,
∵∠M+∠BAF=90°,∠BFA+∠BFM=90°,
∴∠M=∠BFM,
∴BM=BF=x,
在Rt△BGM中,BM=$\sqrt{{x}^{2}+{9}^{2}}$,
由△MBG∽△MFA可得,$\frac{BM}{FM}$=$\frac{BG}{AF}$=$\frac{GM}{AM}$,
∴$\frac{x}{FM}$=$\frac{9}{AF}$=$\frac{\sqrt{{x}^{2}+81}}{2x}$,
∴FM=$\frac{2{x}^{2}}{\sqrt{{x}^{2}+81}}$,AF=$\frac{18x}{\sqrt{{x}^{2}+81}}$,
易知BK=$\frac{1}{2}$FM=$\frac{{x}^{2}}{\sqrt{{x}^{2}+81}}$,
∵$\frac{1}{2}$•AF•BK=$\frac{1}{2}$•BF•AH,
∴AH=$\frac{18{x}^{2}}{{x}^{2}+81}$,
∵△ABH∽△BCF,
∴$\frac{AB}{BE}$=$\frac{AH}{BC}$,
∴$\frac{x}{x+2}$=$\frac{\frac{18{x}^{2}}{{x}^{2}+81}}{x}$,
∴x=15或3(舍弃),
∴BF=15.
点评 本题考查正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会利用参数,构建方程解决问题,属于中考压轴题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题
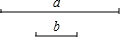 在数学课上,老师提出如下问题:
在数学课上,老师提出如下问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
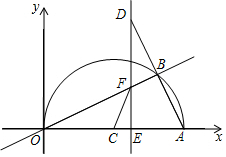 如图,在平面直角坐标系中,点A(20,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.
如图,在平面直角坐标系中,点A(20,0),以OA为直径在第一象限内作半圆C,点B是该半圆周上一动点,连结OB、AB,并延长AB至点D,使DB=AB,过点D作x轴垂线,分别交x轴、直线OB于点E、F,点E为垂足,连结CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
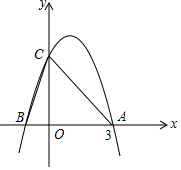 如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com