【题目】如图所示，AB∥CD，AD∥BC，OE＝OF，则图中全等三角形的组数是（ ）
A.3组B.4组C.5组D.6组
【答案】D
【解析】
先根据题意AB∥CD，AD∥BC，可得多对角相等，再利用平行四边形的性质可得线段相等，所以有△AFO≌△CEO，△AOD≌△COB，△FOD≌△EOB，△ACB≌△ACD，△ABD≌△DCB，△AOB≌△COD共6对．
∵AB∥CD，AD∥BC
∴∠ABD＝∠CDB，∠ADB＝∠CDB
又∵BD＝DB
∴△ABD≌△CDB
∴AB＝CD，AD＝BC
∵OA＝OC，OB＝OD
∴△ABO≌△CDO，△BOC≌△DOA
∵OB＝OD，∠CBD＝∠ADB，∠BOF＝∠DOE
∴△BFO≌△DEO
∴OE＝OF
∵OA＝OC，∠COF＝∠AOE
∴△COF≌△AOE
∵AB＝DC，BC＝AD，AC＝AC
∴△ABC≌△DCA，
共6组；
故选：D．
科目：初中数学 来源： 题型：
【题目】如图，已知线段
， 
于点
，且
， 
是射线
上一动点， 
、
分别是
， 
的中点，过点
， 
， 
的圆与
的另一交点
（点
在线段
上），连结
， 
．
（
）当
时，则
的度数为__________．
（
）在点
的运动过程中，当
时，取四边形
一边的两端点和线段
上一点
，若以这三点为顶点的三角形是直角三角形，当
时，则
的值为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知A（3，0），以OA为一边在第一象限内画正方形OABC，D（m，0）为x轴上的一个动点，以BD为一边画正方形BDEF（点F在直线AB右侧）．
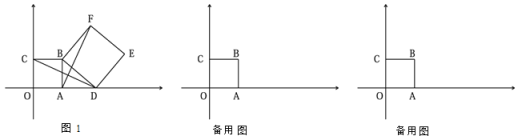
（1）当m＞3时（如图1），试判断线段AF与CD的数量关系，并说明理由．
（2）当AF=5时，求点E的坐标；
（3）当D点从A点向右移动4个单位，求这一过程中F点移动的路程是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．
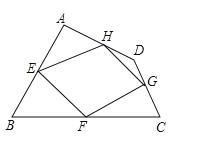
（1）四边形EFGH的形状是什么，并证明你的结论．
（2）当四边形ABCD的对角线满足什么条件时，四边形EFGH是矩形；并利用你给的条件加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
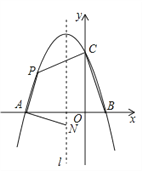
【题目】如图，抛物线
与x轴交于点A和点B（1，0），与y轴交于点C（0，3），其对称轴
为
=–1，P为抛物线上第二象限的一个动点．
（1）求抛物线的解析式并写出其顶点坐标；
（2）当点P的纵坐标为2时，求点P的横坐标；
（3）当点P在运动过程中，求四边形PABC面积最大时的值及此时点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某省计划5年内全部地级市通高铁.某高铁在泰州境内的建设即将展开，现有大量的沙石需要运输.某车队有载质量为8t、10t的卡车共12辆，全部车辆运输一次能运输100t沙石.
（1）求某车队载质量为8t、10t的卡车各有多少辆；
（2）随着工程的进展，某车队需要一次运输沙石165t以上,为了完成任务，准备新增购这两种卡车共7辆，车队有多少种购买方案?请你一一求出.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知四边形ABCD是正方形，点P在直线BC上，点G在直线AD上（P，G不与正方形顶点重合，且在CD的同侧），PD=PG，DF⊥PG于点H，交直线AB于点F，将线段PG绕点P逆时针旋转90°得到线段PE，连结EF．
（1）如图1，当点P与点G分别在线段BC与线段AD上时．
①请直接写出线段DG与PC的数量关系(不要求证明）；
②求证：四边形PEFD是菱形；
（2）如图2，当点P与点G分别在线段BC与线段AD的延长线上时，请猜想四边形PEFD是怎样的特殊四边形，并证明你的猜想．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司有A、B两种型号的客车，它们的载客量、每天的租金如表所示：
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
已知某中学计划租用A、B两种型号的客车共10辆，同时送七年级师生到沙家参加社会实践活动，已知该中学租车的总费用不超过5600元．
(1)求最多能租用多少辆A型号客车？
(2)若七年级的师生共有380人，请写出所有可能的租车方案．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
