
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),交
的左侧),交![]() 轴于点
轴于点![]() ,将直线
,将直线![]() 以点
以点![]() 为旋转中心,顺时针旋
为旋转中心,顺时针旋![]() 转,交
转,交![]() 轴于点
轴于点![]() ,交抛物线于另一点
,交抛物线于另一点![]() .直线
.直线![]() 的解析式为:
的解析式为:![]()
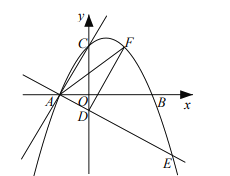
![]() 点
点![]() 是第一象限内抛物线上一点,当
是第一象限内抛物线上一点,当![]() 的面积最大时,在线段
的面积最大时,在线段![]() 上找一点
上找一点![]() (不与
(不与![]() 重合),使
重合),使![]() 的值最小,求出点
的值最小,求出点![]() 的坐标,并直接写出
的坐标,并直接写出![]() 的最小值;
的最小值;
![]() 如图,将
如图,将![]() 沿射线
沿射线![]() 方向以每秒
方向以每秒![]() 个单位的速度平移,记平移后的
个单位的速度平移,记平移后的![]() 为
为![]() ,平移时间为
,平移时间为![]() 秒,当
秒,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的值.
的值.

【答案】(1)点![]() 的坐标为
的坐标为![]() .
.![]() 的最小值为
的最小值为![]() .(2)
.(2)![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
![]() 过点
过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,表示出FK,
,表示出FK,![]() ,根据二次函数的性质即可求解.
,根据二次函数的性质即可求解.
![]() 连接
连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() ,
,![]() ,
,![]() .点
.点![]() 的坐标为
的坐标为![]() .求出点
.求出点![]() 的坐标为
的坐标为![]() .
.
![]()
![]() ,
,![]() ,分三种情况进行讨论即可.
,分三种情况进行讨论即可.
解:![]() 过点
过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() (如答图1),
(如答图1),
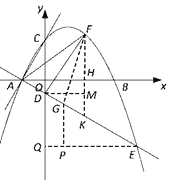
过点![]() 作
作![]() 于点
于点![]() .
.
设点![]() 的坐标为
的坐标为![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 有最大值.
有最大值.
![]() 此时点
此时点![]() 的坐标为
的坐标为![]() .
.
点![]() 是线段
是线段![]() 上一点,作
上一点,作![]() 轴于点
轴于点![]() ,
,![]() 于点
于点![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,此时
,此时![]() 的值最小,
的值最小,
![]() 此时点
此时点![]() 的坐标为
的坐标为![]() .
.
![]() 的最小值为
的最小值为![]() .
.
![]() 连接
连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() (如答图2)
(如答图2)
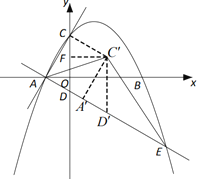
则![]() ,
,![]() ,
,![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
求出点![]() 的坐标为
的坐标为![]() .
.
![]()
![]()
![]() ,
,
![]() 当
当![]() 时,
时,
![]() ,解得
,解得![]() .
.
![]() 当
当![]() 时,
时,
![]() ,解得
,解得![]() (舍去)
(舍去)
![]() 当
当![]() 时,
时,
![]() ,解得
,解得![]() ,
,
综上所述,当![]() 为等腰三角形时,
为等腰三角形时,![]() 或
或![]() 或
或![]() 或
或![]()


科目:初中数学 来源: 题型:
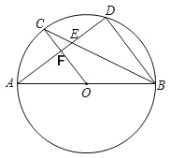
【题目】如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD与BC,OC分别交于E、F
(1)求证:![]() =
=![]() ;
;![]()
(2)若CE=1,EB=3,求⊙O的半径;
(3)若BD=6,AB=10,求D E的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象,下列结论:①2a>b;②a﹣b+c>0;③a<b;④a>c,其中正确的结论是( )
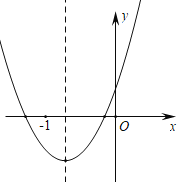
A.①③B.②③C.①④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
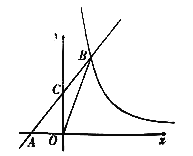
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与轴交于点A(-2.0),与反比例函数y=![]() (m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(1)求反比例函数和一次函数的表达式:
(2)若直线AB与y轴的交点为C.求△OCB的面积
(3)根据图象,直接写出当x>0时,不等式![]() >kx+b的解集.
>kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一批货物准备运往某地,有甲、乙、丙三辆卡车可雇用.已知甲、乙、丙三辆车每次运货量不变,且甲、乙两车单独运完这批货物分别用![]() 次;甲、丙两车合运相同次数,运完这批货物,甲车共运
次;甲、丙两车合运相同次数,运完这批货物,甲车共运![]() 吨;乙、丙两车合运相同次数,运完这批货物乙车共运
吨;乙、丙两车合运相同次数,运完这批货物乙车共运![]() 吨,现甲、乙、丙合运相同次数把这批货物运完,货主应付甲车主的运费为___________ 元.(按每吨运费
吨,现甲、乙、丙合运相同次数把这批货物运完,货主应付甲车主的运费为___________ 元.(按每吨运费![]() 元计算)
元计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正方形
中,正方形![]() 的边长为4,顶点
的边长为4,顶点![]() 在第一象限,点
在第一象限,点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,抛物线
轴上,抛物线![]() 经过点D(-1,0).
经过点D(-1,0).
(1)求点C的坐标;
(2)求抛物线的对称轴;
(3)若抛物线![]() 与正方形
与正方形![]() 的边恰好有三个公共点,求
的边恰好有三个公共点,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达
两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达![]() 地后马上以另一速度原路返回
地后马上以另一速度原路返回![]() 地(掉头的时间忽略不计),乙车到达
地(掉头的时间忽略不计),乙车到达![]() 地以后即停在
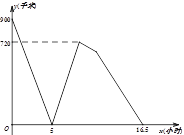
地以后即停在![]() 地等待甲车.如图所示为甲乙两车间的距离
地等待甲车.如图所示为甲乙两车间的距离![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (小时)之间的函数图象,则当乙车到达
(小时)之间的函数图象,则当乙车到达![]() 地的时候,甲车与
地的时候,甲车与![]() 地的距离为__________千米.
地的距离为__________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
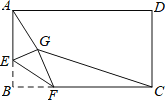
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=![]() ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )
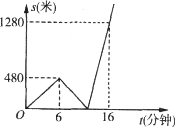
A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com