
【题目】如图,已知Rt△ABC中,∠C=90°,AC=6,BC=8,点E、F分别是边AC、BC上的动点,且EF//AB,点C关于EF的对称点D恰好落在△ABC的内角平分线上,则CD长为__________.
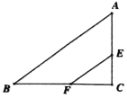
【答案】3或![]()
【解析】
点C关于EF的对称点D恰好落在△ABC的内角平分线上,有两种情况:∠ABC或∠ACB的角平分线;正确画出图形,得出点D即角平分线与AB边高CH的交点,再由角平分线性质可得DH=DG=CH-CD,点C关于EF的对称点D恰好落在∠ABC的角平分线上,利用![]() 列方程即可求出CD.
列方程即可求出CD.
解:i、当点C关于EF的对称点D恰好落在∠ABC的角平分线上时,
过C点作CH⊥EF,交AB于点H,交∠ABC平分线与点D,
∵点C关于EF的对称点D恰好落在∠ABC的内角平分线上,故点D即点C关于EF的对称点,
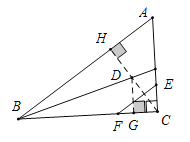
∵∠C=90°,AC=6,BC=8,
∴![]() ,
,
∴![]() ,
,
∵CH⊥EF,EF//AB,
∴CH⊥AB,
∴![]() , ∠BCH=∠A,
, ∠BCH=∠A,
过D点作DG⊥BC,垂足为G,
∵DB平分∠ABC,DH⊥AB,DG⊥BC,
∴DH=DG=CH-CD,
∵![]() ,
,![]() ,
,
∴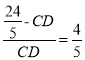 ,解得:
,解得: ![]() ;
;
ii、当点C关于EF的对称点D恰好落在∠BAC的角平分线上时,如图,

同理可得:![]() ,
,
综上所述:点C关于EF的对称点D恰好落在△ABC的内角平分线上,则CD长为3或![]() .
.
故答案为:3或![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
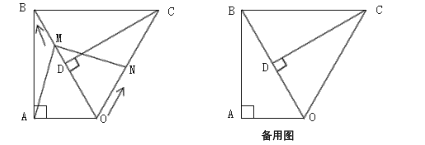
【题目】如图,已知![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速行动,速度为
方向匀速行动,速度为![]() ;同时,点
;同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动,另一个点也停让运动.连接
;当一个点停止运动,另一个点也停让运动.连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() ,解答下列问题:
,解答下列问题:
(1)当![]() 为何值时,
为何值时,![]() 平分
平分![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函教关系式;
的函教关系式;
(3)在运动过程中,当![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(4)在运动过程中,是否存在某一时刻![]() ,使点
,使点![]() 为线段
为线段![]() 的中点?若存在,求出
的中点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接体育理化加试,九(2)班同学到某体育用品商店采购训练用球,已知购买3个A品牌足球和2个B品牌足球需付210元;购买2个A品牌足球和1个B品牌足球需付费130元.(优惠措施见海报)

(1)求A,B两品牌足球的单价各为多少元;
(2)为享受优惠,同学们决定购买一次性购买足球60个,若要求A品牌足球的数量不低于B品牌足球数量的3倍,请你设计一种付费最少的方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,CD是AB边上的中线,点E为线段CD上一点(不与点C、D重合),连接BE,作EF⊥BE与AC的延长线交于点F,与BC交于点G,连接BF.
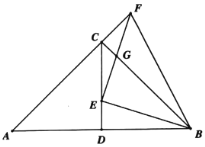
(1)求证:△CFG∽△EBG;
(2)求∠EFB的度数;
(3)求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y1=﹣x2+bx+4.
(1)如图,抛物线与x轴相交于两点(1﹣m,0)、(1+m,0).
①求b的值;
②当n≤x≤n+1时,二次函数有最大值为3,求n的值.
(2)已知直线l:y2=2x﹣b+9,当x≥0时,y1≤y2恒成立,求b的取值范围.
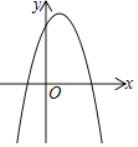
查看答案和解析>>
科目:初中数学 来源: 题型:
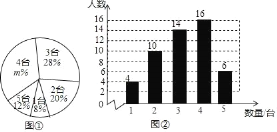
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(Ⅰ)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(Ⅱ)求本次调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
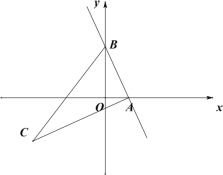
【题目】如图所示,已知直线![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 与点
与点![]() ,点
,点![]() 在第三象限内,且
在第三象限内,且![]() ,
,![]() .
.
(1)当![]() 时,求抛物线的表达式;
时,求抛物线的表达式;
(2)设点![]() 坐标为
坐标为![]() ,试用
,试用![]() 分别表示
分别表示![]() ;
;
(3)记![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com