
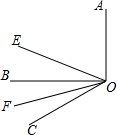
 如图,已知OE,OF分别平分∠AOC,∠BOC,若∠EOF=45°,试判断OA与OB的位置关系,并说明理由.
如图,已知OE,OF分别平分∠AOC,∠BOC,若∠EOF=45°,试判断OA与OB的位置关系,并说明理由. 分析 利用角平分线的定义得到∠EOC=$\frac{1}{2}$∠AOC∠FOC=$\frac{1}{2}$∠BOC,则可变形出∠EOF=$\frac{1}{2}$∠AOB,于是得到∠AOB=2∠EOF=90°,所以可判断OA⊥OB.
解答 解:OA⊥OB.
理由如下:∵OE、OF分别平分∠AOC,∠BOC,
∴∠EOC=$\frac{1}{2}$∠AOC∠FOC=$\frac{1}{2}$∠BOC,
又∵∠EOF=∠EOC-∠FOC=$\frac{1}{2}$∠AOC-$\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOC-∠BOC)=$\frac{1}{2}$∠AOB
∴∠AOB=2∠EOF=2×45°=90°
∴OA⊥OB.
点评 本题考查了角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.性质:若OC是∠AOB的平分线,则∠AOC=∠BOC.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
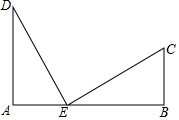 如图.公路AB的同侧有两所学校C、D,学校D到公路的距离DA=3km,学校C到公路的距离CB=2km,已知AB=5km.现在要在公路AB上建一个公交车站E,使车站E到学校C、D的距离相等,则AE为多少?
如图.公路AB的同侧有两所学校C、D,学校D到公路的距离DA=3km,学校C到公路的距离CB=2km,已知AB=5km.现在要在公路AB上建一个公交车站E,使车站E到学校C、D的距离相等,则AE为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com