
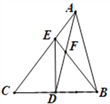
【题目】如图,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )
A. 1个 B. 4个 C. 3个 D. 2个
【答案】C
【解析】∵D是BC的中点,且DE⊥BC,
∴DE是BC的垂直平分线,CD=BD,
∴CE=BE,故本答案正确;
∴∠C=∠7
∵AD=AB,
∴∠8=∠ABC=∠6+∠7,
∵∠8=∠C+∠4,
∴∠C+∠4=∠6+∠7,
∴∠4=∠6,即∠CAD=∠ABE,故本答案正确;
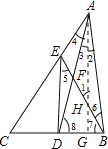
作AG⊥BD于点G,交BE于点H,
∵AD=AB,DE⊥BC,
∴∠2=∠3,DG=BG=![]() BD,DE∥AG,
BD,DE∥AG,
∴CDE△∽△CGA,△BGH∽△BDE,EH=BH,∠EDA=∠3,∠5=∠1,
∴CD:CG=DE:AG,HG=![]() DE,
DE,
设DG=x,DE=y,则GB=x,CD=2x,CG=3x
∴2x:3x=2y:AG,
解得:AG=3y,HG=y
∴AH=2y
∴DE=AH,且∠EDA=∠3,∠5=∠1
∴DEF△≌△AHF
∴EF=HF=![]() EH,且EH=BH,
EH,且EH=BH,
∴EF:BF=1:3,
∴S△ABF=3S△AEF,
∵S△DEF=S△AEF,
∴S△ABF=3S△DEF,故本答案正确;
∵∠1=∠2+∠6,且∠4=∠6,∠2=∠3,
∴∠5=∠3+∠4,
∴∠5≠∠4,
∴△DEF∽△DAE,不成立,故本答案错误,
综上所述:正确的答案有3个,
故选C.


科目:初中数学 来源: 题型:
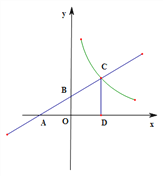
【题目】已知一次函数![]() 的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数
的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数![]() 的图象相交于点C,OA=3.
的图象相交于点C,OA=3.
(1)求一次函数的解析式和点B的坐标;
(2)作CD⊥x轴,垂足为D,若![]() =1:3,求反比例函数
=1:3,求反比例函数![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
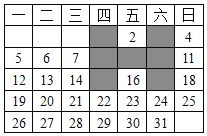
【题目】如图,表中给出的是某月的月历,任意选取“![]() ”型框中的
”型框中的![]() 个数(如阴影部分所示).请你运用所学的数学知识来研究,则这
个数(如阴影部分所示).请你运用所学的数学知识来研究,则这![]() 个数的和不可能是( )
个数的和不可能是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上A、B、C三点所代表的数分别是a、b、1.且|a﹣1|﹣|1﹣b|=|a﹣b|.下列四个选项中,有( )个能表示A、B、C三点在数轴上的位置关系?
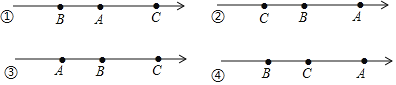
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
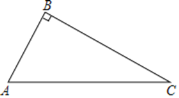
【题目】如图,在△ABC中,∠ABC=90°,
(1)按下列要求完成尺规作图:作线段AC的垂直平分线l,交AC于点O;连接BO并延长至D,使得OD=OB;连接DA、DC(保留作图痕迹,请标明字母);
(2)判断四边形ABCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
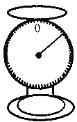
【题目】某市场的公平秤如图,把10千克的菜放到秤上,指示盘上的指针转了180°.
(1)如果把2.75千克的菜放在秤上,指针转过多少度?
(2)如果称好0.5千克的菜没有拿走,再把一捆菜放在秤上,指针共转了![]() 那么,后放上的这捆菜有多少千克?
那么,后放上的这捆菜有多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
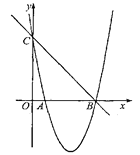
【题目】如图,已知抛物线y=x2+bx+c的图像与x轴的一个交点为A(1,0),另一个交点为B,且与y轴交于点C(0,5).
(1)求直线BC及抛物线的解析式;
(2)若点M是抛物线在x轴下方图像上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图像上任意一点,以BC为边作□CBPQ,设□CBPQ的面积为S1,△ABN的面积为S2,且S1=6S2,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
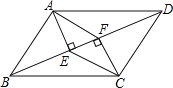
【题目】如图,在四边形ABCD中,AB∥CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AC与BD互相平分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子
产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:
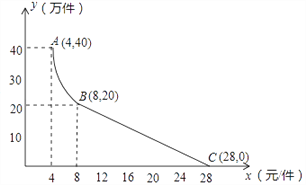
每年的年销售量![]() (万件)与销售价格
(万件)与销售价格![]() (元/件)的关系如图所示,其中AB为反比例函数图象的一
(元/件)的关系如图所示,其中AB为反比例函数图象的一
部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为![]() (万元).(注:若上一
(万元).(注:若上一
年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出![]() (万件)与
(万件)与![]() (元/件)之间的函数关系式;
(元/件)之间的函数关系式;
(2)求出第一年这种电子产品的年利润![]() (万元)与
(万元)与![]() (元/件)之间的函数关系式,并求出第一年年利润的最大值;
(元/件)之间的函数关系式,并求出第一年年利润的最大值;
(3)假设公司的这种电子产品第一年恰好按年利润![]() (万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格
(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格![]() (元)定在8元以上(
(元)定在8元以上(![]() ),当第二年的年利润不低于103万元时,请结合年利润
),当第二年的年利润不低于103万元时,请结合年利润![]() (万元)与销售价格
(万元)与销售价格![]() (元/件)的函数示意图,求销售价格
(元/件)的函数示意图,求销售价格![]() (元/件)的取值范围.
(元/件)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com