【答案】
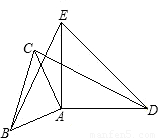
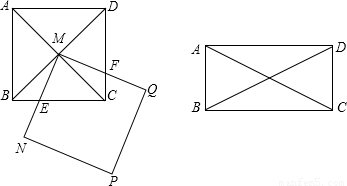
分析:(1)求简单的线段相等,可证线段所在的三角形全等;故M分别作MG⊥BC于G,MH⊥CD于H,易得MG=MH,而∠EMG、∠FMH都是∠GMF的余角,由此可证得∠EMG=∠FMH,即可证得△MGE≌△MHF,由此得证.
(2)此题要分四种情况讨论:
①当MN交BC于点E,MQ交CD于点F时;此种情况与(1)类似,不同的是(1)题用到的是全等,而此题运用的是相似,过点M作MG⊥BC于点G,MH⊥CD于点H,通过证△MGE∽△MHF,得到关于ME、MF、MG、MH的比例关系式,联立矩形的性质及BC、AB的比例关系,即可求得ME、MF的比例关系;
②当MN的延长线交AB于点E,MQ交BC于点F时.解法同①;
③当MN、MQ两边都交边BC于E、F时,过M作MH⊥BC于H,由于M是AC的中点,且已知AB的长,即可求得MH=1,在Rt△EMF中,MH⊥EF,易证得△MEH∽△FEM,△FMH∽△FEM.可得
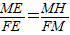
,
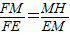
.将MH=1代入上述两式,然后联立勾股定理即可得到ME、MF的关系式;
④当MN交BC边于E点,MQ交AD于点F时.可延长EM交BC于G,易证得△MED≌△MGB,即可得ME=MG,那么这种情况下与③完全相同,即可得解.
解答: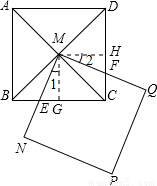
(1)证明:过点M作MG⊥BC于点G,MH⊥CD于点H.
∴∠MGE=∠MHF=90°.
∵M为正方形对角线AC、BD的交点,∴MG=MH.
又∵∠1+∠GMQ=∠2+∠GMQ=90°,
∴∠1=∠2.
在△MGE和△MHF中
∠1=∠2,
MG=MH,
∠MGE=∠MHF.
∴△MGE≌△MHF.
∴ME=MF.(3分)
(2)解:①当MN交BC于点E,MQ交CD于点F时.
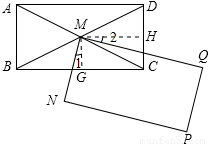
过点M作MG⊥BC于点G,MH⊥CD于点H.
∴∠MGE=∠MHF=90°.
∵M为矩形对角线AC、BD的交点,
∴∠1+∠GMQ=∠2+∠GMQ=90°.
∴∠1=∠2.
在△MGE和△MHF中,
∠1=∠2
∠MGE=∠MHF
∴△MGE∽△MHF.
∴

.
∵M为矩形对角线AB、AC的交点,∴MB=MD=MC
又∵MG⊥BC,MH⊥CD,∴点G、H分别是BC、DC的中点.
∵BC=2AB=4,
∴
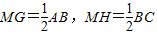
.
∴
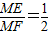
.(4分)
②当MN的延长线交AB于点E,MQ交BC于点F时.
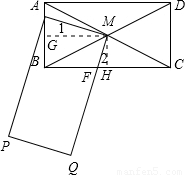
过点M作MG⊥AB于点G,MH⊥BC于点H.
∴∠MGE=∠MHF=90°.
∵M为矩形对角线AC、BD的交点,
∴∠1+∠GMQ=∠2+∠GMQ=90°.
∴∠1=∠2.
在△MGE和△MHF中,
∠1=∠2,
∠MGE=∠MHF.
∴△MGE∽△MHF.
∴
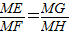
.
∵M为矩形对角线AC、BD的交点,
∴MB=MA=MC.
又∵MG⊥AB,MH⊥BC,∴点G、H分别是AB、BC的中点.
∵BC=2AB=4,∴

.
∴
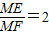
.(5分)
③当MN、MQ两边都交边BC于E、F时.
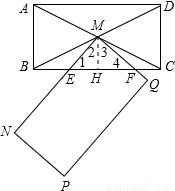
过点M作MH⊥BC于点H.
∴∠MHE=∠MHF=∠NMQ=90°.
∴∠1=∠3,∠2=∠4.
∴△MEH∽△FEM,△FMH∽△FEM.
∴
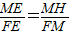
,
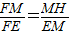
.
∵M为矩形对角线AC、BD的交点,
∴点M为AC的中点.
又∵MH⊥BC,
∴点M、H分别是AC、BC的中点.
∵BC=2AB=4,
∴AB=2.
∴MH=1.
∴
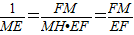
,
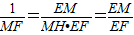
.
∴
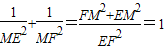
.(6分)
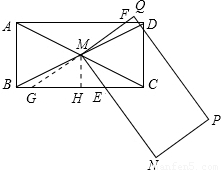
④当MN交BC边于E点,MQ交AD于点F时.
延长FM交BC于点G.
易证△MFD≌△MGB.∴MF=MG.
同理由③得
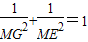
.
∴
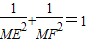
.(7分)
综上所述:ME与MF的数量关系是
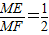
或
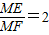
或
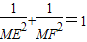
.
点评:此题考查了正方形、矩形的性质,全等三角形、相似三角形的判定和性质以及勾股定理等知识的综合应用;由于(2)题的情况较多,做到不漏解是此题的难点.

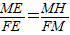 ,
,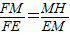 .将MH=1代入上述两式,然后联立勾股定理即可得到ME、MF的关系式;
.将MH=1代入上述两式,然后联立勾股定理即可得到ME、MF的关系式; (1)证明:过点M作MG⊥BC于点G,MH⊥CD于点H.
(1)证明:过点M作MG⊥BC于点G,MH⊥CD于点H.
 .
.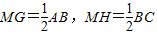 .
.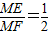 .(4分)
.(4分) 过点M作MG⊥AB于点G,MH⊥BC于点H.
过点M作MG⊥AB于点G,MH⊥BC于点H.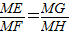 .
. .
.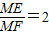 .(5分)
.(5分)
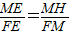 ,
,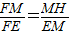 .
.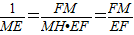 ,
,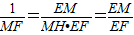 .
.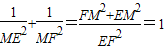 .(6分)
.(6分) ④当MN交BC边于E点,MQ交AD于点F时.
④当MN交BC边于E点,MQ交AD于点F时.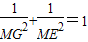 .
.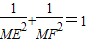 .(7分)
.(7分)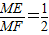 或
或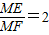 或
或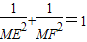 .
.

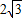 ,0),B(
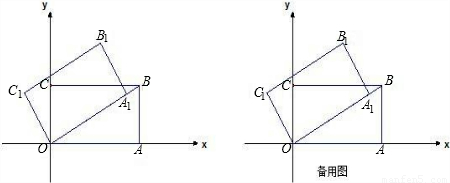
,0),B(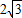 ,2).把矩形OABC逆时针旋转30°得到矩形OA1B1C1,
,2).把矩形OABC逆时针旋转30°得到矩形OA1B1C1,