
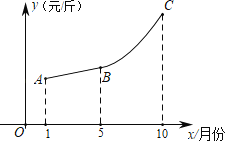
����Ŀ�����������۸�һֱ����һ·�����������һ�����ƣ��Բ��𣡽��գ�����ʦͨ����ز����˽2019��1�µ�10�º��ݸ����е��������ƽ���ۼۣ�����������ͼ��ʾ�ĺ���ͼ������1�·ݵ�5�·ݵ������ۼ�y���·�x֮��Ĺ�ϵ�����߶�AB��5�·ݵ�10�·ݵ������ۼ�y���·�x֮��Ĺ�ϵ����������BC����֪��A��1��16������B��5��17������C��10��42�����ҵ�B�������ߵĶ��㣮
��1�����߶�AB��������BC�Ľ���ʽ��
��2����֪1�·ݵ�5�·������ƽ������Ϊ13Ԫ/�5�·ݵ�10�·������ƽ������z���·�x֮��Ĺ�ϵΪz��3x��2��xΪ��������������ÿ����һ�������õ�����Ϊw������1�µ�10��w�����Ƕ���Ԫ��
���𰸡���1���߶�AB�Ľ���ʽΪ��y��![]() x+
x+![]() ��������BC�Ľ���ʽΪ��y����x��5��2+17����2��1�µ�10��w������2Ԫ��
��������BC�Ľ���ʽΪ��y����x��5��2+17����2��1�µ�10��w������2Ԫ��
��������
��1�����߶�AB�Ľ���ʽΪ��y��kx+b����������BC�Ľ���ʽΪ��y��a��x��5��2+17���ⷽ�̻��鼴�ɵõ����ۣ�
��2����1��x��5ʱ����5��x��10ʱ�����ݶ��κ��������ʼ��ɵõ����ۣ�
�⣺��1�����߶�AB�Ľ���ʽΪ��y��kx+b��
�ߵ�A��1��16������B��5��17����
��![]()
��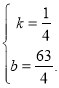
���߶�AB�Ľ���ʽΪ��y��![]() x+
x+![]() ��
��
�ߵ�B�������ߵĶ��㣬
����������BC�Ľ���ʽΪ��y��a��x��5��2+17��
��C��10��42������ã�42��a��10��5��2+17��
��ã�a��1��
��������BC�Ľ���ʽΪ��y����x��5��2+17��
��2����1��x��5ʱ��w��![]() x+
x+![]() ��13��
��13��![]() x+
x+![]() ��
��
�ʵ�x��1ʱ��w����СֵΪ3��
��5��x��10ʱ��w����x��5��2+17����3x��2������x��6.5��2+1.75��
��x��������
�൱x��6��7ʱ��w����Сֵ2��
������������x��6��7ʱ��w����Сֵ2��
��1�µ�10��w������2Ԫ.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ϊ����ԭ��һ��¥����֣�ݻ�չ����(�׳ơ������ס�)�����ڷ羰�续���������,����֣�ݹ۹���ο���Ӱ����Ѿ���,ѧ�������Ǻ���֪ʶ��,����������ͬѧ�������Լ�ѧ����֪ʶ�����������ס��ĸ߶������ƶ��˲�������,�����ÿ���ʱ�������ʵ�ز���,������Ŀ��������±�
���������С������ϱ��еIJ�������,���֣�ݻ�չ���ݵĸ߶�.
(�����:sin40���0.64,cos40���0.77,tan40���0.84,�����������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪���������ε�������ƽ���߽���һ�㣬������Ϊ�����ε�����(����������Բ��Բ��).���ڹ涨������ı��ε��ĸ��ǵĽ�ƽ���߽���һ�㣬���ǰ������Ҳ��Ϊ���ı��ε�������.
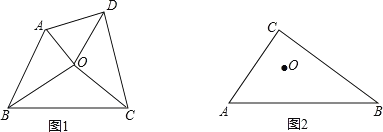
(1)�Ծٳ�һ�������ĵ��ı���.
(2)��ͼ1����֪��O���ı���ABCD�����ģ���֤��AB+CD=AD+BC.
(3)��ͼ2��Rt��ABC�У���C=90��.O����ABC������.��ֱ��DE�ر�AC��BC�ڵ�D.E����O��Ȼ���ı���ABED������.������ֱ��DE�ɻ�������?����ͼ2�л���һ������������ֱ��DE������˵������.
(4)����(3)�У���AC=3��BC=4������������һ��ֱ��DE��AB����DE�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�Ƶ�C˳ʱ����ת90��õ���EDC������A��D��E��ͬһ��ֱ���ϣ���ACB=20�㣬���ADC�Ķ�����![]() ����
����![]()
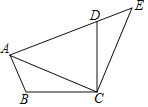
A. 55�� B. 60�� C. 65�� D. 70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ˮƽ���õ����ǰ�ABC��ֱ�Ƕ���A��ʱ����ת���õ���AB'C'�����Ტ�ӳ�BB'��C'C�ཻ�ڵ�P�����С�ABC��30����BC��4��
��1������B'C'�е�Ϊ��D������PD����PD��_____��
��2�����ǵ�P��ֱ��AC'�ľ���Ϊd����d�����ֵΪ_____��
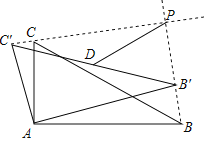
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ȱ����ΰ�AB��Ϊ3��,���ΰ�AB��֧�ŵ�O�������ϵĵ�H�ľ��OH=0.6�ס������ΰ�AB��һ���˵�A��������ʱ,AB������ϵ�ֱ��AH�ļнǡ�OAH�Ķ���Ϊ30��.

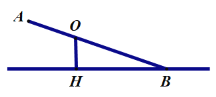
��1����AB����һ���˵�B��������ʱ(����ͼ��,���ΰ�AB��ֱ��BH�ļнǡ�ABH������ֵ�Ƕ���?
��2����AB����һ���˵�B��������ʱ(����ͼ),��A��ֱ��BH�ľ����Ƕ�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
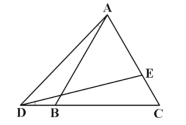
����Ŀ����ͼ����ABCD�У�BFƽ�֡�ABC��AD�ڵ�F,CEƽ�֡�DCB��AD�ڵ�E,BF��CE�ཻ�ڵ�P.

(1)��֤��AE=DF.
(2)��֪AB=4,AD=5.
����![]() ��ֵ��
��ֵ��
�����ı���ABPE��������BPC�����֮��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ�������![]() �У�
��![]() ����D��
����D��![]() �ӳ�����һ�㣬��
�ӳ�����һ�㣬��![]() ����E��ֱ��
����E��ֱ��![]() �ϣ���
�ϣ���![]() ʱ��
ʱ��![]() �ij�Ϊ_____.
�ij�Ϊ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
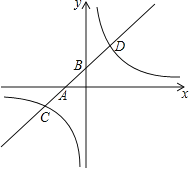
����Ŀ����ͼ��һ�κ���y1=k1x+b��k1��0����ͼ��ֱ���x�ᣬy���ཻ�ڵ�A��B���뷴��������y2=![]() ��ͼ���ཻ�ڵ�C����4����2����D��2��4����
��ͼ���ཻ�ڵ�C����4����2����D��2��4����
��1����һ�κ����ͷ����������ı���ʽ��
��2����xΪ��ֵʱ��y1��0��
��3����xΪ��ֵʱ��y1��y2����ֱ��д��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com