
【题目】已知:等腰△ABC中,AB=AC,点D是直线AC上一动点,点E在BD的延长线上,且AB=AE,∠CAE的角平分线所在的直线交BE于F,连结CF. 
(1)如图1,当点D在线段AC上时,求证:∠ABE=∠ACF;
(2)如图2,当∠ABC=60°且点D在线段AC上时,求证:AF+EF=FB.(提示:将线段FB拆分成两部分)
(3)①如图3,当∠ABC=45°其点D在线段AC上时,线段AF、EF、FB仍有(2)中的结论吗?若有,加以证明;若没有,则有怎样的数量关系,直接写出答案即可.
②如图4,当∠ABC=45°且点D在CA的延长线时,请你按题意将图形补充完成.并直接写出线段AF、EF、FB的数量关系.
【答案】
(1)证明:如图1,
∵AF平分∠CAE,
∴∠EAF=∠CAF,
∵AB=AC,AB=AE,
∴AE=AC,
在△ACF和△AEF中,
 ,
,
∴△ACF≌△AEF(SAS),
∴∠E=∠ACF,
∵AB=AE,
∴∠E=∠ABE,
∴∠ABE=∠ACF

(2)证明:在FB上截取BM=CF,连接AM,如图2,
∵△ACF≌△AEF,
∴EF=CF,∠E=∠ACF=∠ABM,
在△ABM和△ACF中,
 ,
,
∴△ABM≌△ACF(SAS),
∴AM=AF,∠BAM=∠CAF,
∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=60°,
∴∠MAF=∠MAC+∠CAF=∠MAC+∠BAM=∠BAC=60°,
∵AM=AF,
∴△AMF为等边三角形,
∴AF=AM=MF,
∴AF+EF=BM+MF=FB,
即AF+EF=FB

(3)证明:①线段AF、EF、FB不是(2)中的结论,线段AF、EF、FB的数量关系为 ![]() AF+EF=FB,理由如下:
AF+EF=FB,理由如下:
在FB上截取BM=CF,连接AM,如图3,
∵△ACF≌△AEF,
∴EF=CF=BM,∠E=∠ACF=∠ABM,
在△ABM和△ACF中,
 ,
,
∴△ABM≌△ACF(SAS),
∴AM=AF,∠BAM=∠CAF,
∵AB=AC,∠ABC=45°,
∴△ABC是等腰直角三角形,
∴∠BAC=90°,
∴∠MAF=∠MAC+∠CAF=∠MAC+∠BAM=∠BAC=90°,
∵AM=AF,
∴△AMF为等腰直角三角形,
∴MF= ![]() AF,
AF,
∴FB=BM+MF=EF+ ![]() AF,
AF,
即 ![]() AF+EF=FB;
AF+EF=FB;
②如图4,在CF上截取CG=BF,连接AG,

在△AFE和△AFC中,
 ,
,
∴△AFE≌△AFC(SAS),
∴FE=FC,∠FEA=∠FCA,
∵AB=AE,
∴∠ABF=∠AEF=∠ACF,
在△ABF和△ACG中,
 ,
,
∴△ABF≌△ACG(SAS),
∴AG=AF,∠FAB=∠GAC,
∵AB=AC,∠ABC=45°,
∴∠BAC=90°,
∴FAG=90°,
∴△AFG是等腰直角三角形,
∴FG= ![]() AF,
AF,
∵CF=CG+GF,
∴CF=BF+ ![]() AF,
AF,
∴EF=BF+ ![]() AF
AF

【解析】(1)证△EAF≌△CAF,推出EF=CF,∠E=∠ACF,根据等腰三角形性质推出∠E=∠ABE,即可得出答案;(2)在FB上截取BM=CF,连接AM,证△ABM≌△ACF,推出EF=FC=BM,AF=AM,推出△AMF是等边三角形,推出MF=AF,即可得出答案;(3)①在FB上截取BM=CF,连接AM,证△ABM≌△ACF,推出EF=FC=BM,AF=AM,推出△AMF是等腰直角三角形,推出MF= ![]() AF,即可得出答案;
AF,即可得出答案;
②只需在CF上截取CG=BF,先证△AFE≌△AFC,得出CF=EF,再证△ABF≌△ACG,得出△AFG是等腰直角三角形,然后结论显然.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有以下两种摆放方式: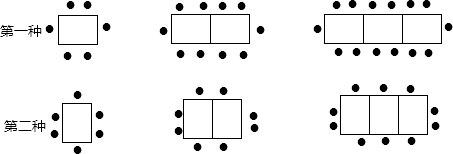
(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=mx﹣4m(m是常数,且m≠0)的图象分别交x轴、y轴于点M,N,线段MN上两点A,B(点B在点A的右侧),作AA1⊥x轴,BB1⊥x轴,且垂足分别为A1 , B1 , 若OA1+OB1>4,则△OA1A的面积S1与△OB1B的面积S2的大小关系是( )
A.S1>S2
B.S1=S2
C.S1<S2
D.不确定的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道:|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:![]()
(1)数轴上表示5与﹣2两点之间的距离是 ,
(2)数轴上表示x与2的两点之间的距离可以表示为 .
(3)如果|x﹣2|=5,则x= .
(4)同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+3|+|x﹣1|=4,这样的整数是 .
(5)由以上探索猜想对于任何有理数x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b交x轴于点(-5,0),则关于x的方程ax+b=0的解是( )
A. x=5 B. x=-5 C. x=0 D. 无法求解
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com