
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E交DC于点N.
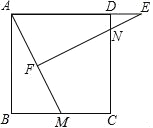
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
【答案】(1)证明见解析;(2)4.9.
【解析】
试题分析:(1)由正方形的性质得出AB=AD,∠B=90°,AD∥BC,得出∠AMB=∠EAF,再由∠B=∠AFE,即可得出结论;
(2)由勾股定理求出AM,得出AF,由△ABM∽△EFA得出比例式,求出AE,即可得出DE的长.
试题解析:(1)∵四边形ABCD是正方形,
∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,
∴∠AFE=90°,
∴∠B=∠AFE,
∴△ABM∽△EFA;
(2)解:∵∠B=90°,AB=12,BM=5,
∴AM=![]() =13,AD=12,
=13,AD=12,
∵F是AM的中点,
∴AF=![]() AM=6.5,
AM=6.5,
∵△ABM∽△EFA,
∴![]() ,
,
即![]() ,
,
∴AE=16.9,
∴DE=AE-AD=4.9.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有( )

A. 4个 B. 5个 C. 6个 D. 7个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场文具部的某种毛笔每支售价25元,书法练习本每本售价5元。该商场为促销制定了两种优惠办法。
A种办法:卖一支毛笔就赠送一本书法练习本;
B种办法:按购买金额打九折付款。
某校欲为校书法兴趣小组购买这种毛笔10支,书法练习本x(x![]() )本。
)本。
(1)写出每本优惠办法实际付款金额y(元)与x(本)之间的函数关系式;
(2)比较购买同样多的书法练习本时,按那种优惠办法付款更省钱。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算多项式-2x(3x-2)2+3除以3x-2后,所得商式与余式两者之和为何?( )
A.-2x+3
B.-6x2+4x
C.-6x2+4x+3
D.-6x2-4x+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.
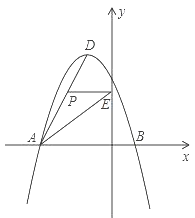
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com