
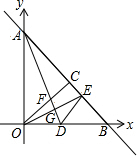
 如图,在平面直角坐标系中,直线AB与坐标轴分别交于A、B两点,已知点A的坐标为(0,8),点B的坐标为(8,0),OC、AD均是△OAB的中线,OC、AD相交于点F,OE⊥AD于G交AB于E.
如图,在平面直角坐标系中,直线AB与坐标轴分别交于A、B两点,已知点A的坐标为(0,8),点B的坐标为(8,0),OC、AD均是△OAB的中线,OC、AD相交于点F,OE⊥AD于G交AB于E.分析 (1)先求出OA,OB进而求出OC,再用待定系数法求出直线AB的解析式,设出点C的坐标,即可得出结论;
(2)先判断出∠AOC=∠OBA,再利用互余判断出∠OAD=∠EOD,即可得出结论;
(3)先确定出OE的解析式,进而求出点E的坐标,即可求出直线DE的解析式,进而判断出OA=OM,即可得出结论.
解答 解:(1)A(0,8),B(0,8),
∴AB=8$\sqrt{2}$,OA=OB,
∴△AOB是等腰直角三角形,
∵OC是△AOB的中线,
∴OC=$\frac{1}{2}$AB=4$\sqrt{2}$,
设直线AB的解析式为y=kx+b,
∵B(8,0),A(0,8),
∴$\left\{\begin{array}{l}{8k+b=0}\\{b=8}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-1}\\{b=8}\end{array}\right.$,
∴直线AB的解析式为y=-x+8,
设点C(m,-m+8),OC=$\sqrt{{m}^{2}+(-m+8)^{2}}$=4$\sqrt{2}$,
∴m=4
∴C(4,4);
(2)由(1)知,OC是等腰直角三角形的斜边的中线,
∴∠AOC=45°=∠OBA,
∵OE⊥AD,
∴∠EOD+∠ODA=90°,
∵∠ADO+∠OAD=90°,
∴∠OAD=∠EOD,
在△AOF和△OBE中,$\left\{\begin{array}{l}{∠AOF=∠OBE}\\{OA=OB}\\{∠OAF=∠BOE}\end{array}\right.$,
∴△AOF≌△OBE;
(3)如图,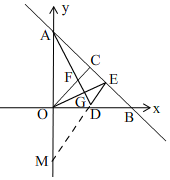 ∵AD是△AOB的中线,
∵AD是△AOB的中线,
∴OD=BD,
∵B(8,0),
∴D(4,0),
∴直线AD的解析式为y=-2x+8,
∵OE⊥AD,
∴直线OE的解析式为y=$\frac{1}{2}$x,
∵点E在直线AB上,
∴$\left\{\begin{array}{l}{y=-x+8}\\{y=\frac{1}{2}x}\end{array}\right.$,解得,$\left\{\begin{array}{l}{x=\frac{16}{3}}\\{y=\frac{8}{3}}\end{array}\right.$,
∴E($\frac{16}{3}$,$\frac{8}{3}$),
∵D(4,0),
∴直线DE的解析式为y=2x-8,
∴OM=8,
∴OA=OM,
∵OB⊥OA,
∴AD=MD,
∴∠ADO=∠MDO.
∵∠EDB=∠MDO,
∴∠ADO=∠EDB.
点评 此题是一次函数综合题,主要考查了待定系数法,全等三角形的判定和性质,等腰三角形的判定和性质,解(1)的关键是求出OC,解(2)的关键是判断出∠OAD=∠EOD,解(3)的关键是确定出点E的坐标.


科目:初中数学 来源: 题型:解答题
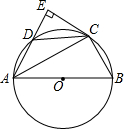 已知:如图,四边形ABCD内接于⊙O,AB是⊙O的直径,CE切⊙O于C,AE⊥CE,交⊙O于D.
已知:如图,四边形ABCD内接于⊙O,AB是⊙O的直径,CE切⊙O于C,AE⊥CE,交⊙O于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学举行“中国梦•校园好声音”歌手大赛,根据初赛成绩,高、初中部各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
某中学举行“中国梦•校园好声音”歌手大赛,根据初赛成绩,高、初中部各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.| 平均数(分) | 中位数(分) | 众数(分) | |
| 初中部 | 85 | 85 | 85 |
| 高中部 | 85 | 80 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
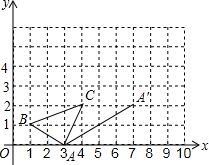 如图,在平面直角坐标系中,△ABC的三个顶点的位置如图所示,现将△ABC沿AA′的方向平移,使得点A移至图中的点A′的位置.
如图,在平面直角坐标系中,△ABC的三个顶点的位置如图所示,现将△ABC沿AA′的方向平移,使得点A移至图中的点A′的位置.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{-a-1}{a+1}$=-$\frac{a-1}{a+1}$ | B. | $\frac{m}{{m}^{2}+1}$=$\frac{1}{m+1}$ | C. | $\frac{{x}^{2}-1}{x-1}$=x-1 | D. | $\frac{a}{a-1}$-$\frac{1}{a-1}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com