练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．先化简，再求值：（a+b）2-2a（b+1）-a2b÷b，其中a=$\frac{1}{2}$，b=$\sqrt{3}$．

    分析 先算乘法和除法，再合并同类项，最后代入求出即可．

    解答 解：（a+b）2-2a（b+1）-a2b÷b
    =a2+2ab+b2-2ab-2a-a2
    =b2-2a，
    当a=$\frac{1}{2}$，b=$\sqrt{3}$时，原式=（$\sqrt{3}$）2-2×$\frac{1}{2}$=2．

    点评 本题考查了整式的混合运算和求值，能正确根据整式的混合运算法则进行化简是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．已知x=$\frac{\sqrt{2}+1}{\sqrt{2}-1}$，y=$\frac{\sqrt{2}-1}{\sqrt{2}+1}$，求下列各式的值
    （1）x2-y2
    （2）$\frac{y}{x}$+$\frac{x}{y}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

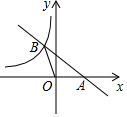    7．如图，直线y=-$\frac{1}{2}$x+b与x轴交于点A，与双曲线y=-$\frac{4}{x}$（x＜0）交于点B，若S△AOB=2，则b的值是（　　）
    A．4B．3C．2D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．袋子中有红球、白球共10个，这些球除颜色外都相同，将袋中的球搅匀，从中随机摸出一个球，记下颜色后再放回袋中，不断重复这一过程，摸了100次后，发现有30次摸到红球，请你估计这个袋中红球约有3个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

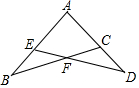    11．如图，△ABC、△ADE中，C、E两点分别在AD、AB上，且BC与DE相交于F点，若∠A=90°，∠B=∠D=30°，AC=AE=1，则四边形AEFC的周长为何（　　）
    A．2$\sqrt{2}$B．2$\sqrt{3}$C．2+$\sqrt{2}$D．2+$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

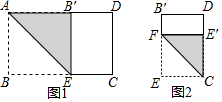    1．矩形纸片ABCD中，AD=10，AB=a（5＜a＜10）
    第1次操作：把该矩形的短边掀起，按图1那样折叠，使点B落在AD边上的B′处，折痕为AE，沿EB′剪下，剩下一个矩形B′ECD，此时ABEB′是正方形，B′D=10-a；
    第二次操作：把矩形B′ECD的短边掀起，按图2那样折叠，使点E落在CD边上的E′处，折痕为CF，沿FE剪下，剩下一个矩形B′FE′D，此时E′D=（用含a的代数式表示）…
    第n次操作后，剩下的矩形为正方形，则操作停止．
    若n=3，则a=2或$\frac{15}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：$\sqrt{16}$-（-1）2018+$\root{3}{-8}$+|-1|

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

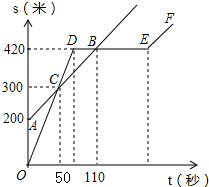    5．某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体，到达起点后小明做了一会准备活动朱老师先跑，当小明出发时，朱老师已经距起点200米了，他们距起点的距离s（米）与小明出发的时间t（秒）之间的关系如图所示（不完整）．根据图中给出的信息，解答下列问题：
    （1）在上述变化过程中，自变量是自变量为小明出发的时间t，因变量是因变量为距起点的距离s；
    （2）朱老师的速度为2米/秒；小明的速度为6米/秒；
    （3）小明与朱老师相遇2次，相遇时距起点的距离分别为300或420米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

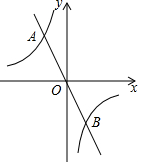    6．如图，在平面直角坐标系中，点A是第二象限内双曲线y=-$\frac{2}{x}$上一点，直线AO与双曲线的另一个交点为B．
    （1）当点A的坐标为（-1，2）时，请计算AB的长；
    （2）当AB的长最小时，请直接写出点A的坐标．

    查看答案和解析>>

    同步练习册答案