
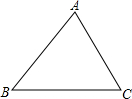
 如图,在△ABC中,AB=9cm,AC=6cm,D是线段AB的一点,AD=3,点E时线段AC上的任意一点,当AE为多少时,△ADE与△ABC相似?
如图,在△ABC中,AB=9cm,AC=6cm,D是线段AB的一点,AD=3,点E时线段AC上的任意一点,当AE为多少时,△ADE与△ABC相似? 分析 分两种情况:①当$\frac{AD}{AB}=\frac{AE}{AC}$时,得出AE=2;②当$\frac{AD}{AC}=\frac{AE}{AB}$时,得出AE=4.5;即可得出结果.
解答 解:∵∠A=∠A,
∴△ADE与△ABC相似,分两种情况:
如图所示: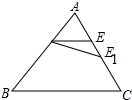
①当$\frac{AD}{AB}=\frac{AE}{AC}$时,
即$\frac{3}{9}=\frac{AE}{6}$,
解得:AE=2;
②当$\frac{AD}{AC}=\frac{AE}{AB}$时,
即$\frac{3}{6}=\frac{AE}{9}$,
解得:AE=4.5.
综上所述:当AE=2或AE=4.5时,△ADE与△ABC相似.
点评 本题考查了相似三角形的判定方法;熟练掌握三角形相似的判定方法,根据图形的特点进行分类讨论是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 某长方形广场除四角外都是空地,四角都是一块半径相同的四分之一圆的草坪,若圆形草坪的半径为r,长方形的长为a,宽为b,请用整式表示空地的面积,并指出这个整式是单项式还是多项式.若是单项式,指出它的系数;若是多项式,指出它有几项,各项的系数分别是多少?
某长方形广场除四角外都是空地,四角都是一块半径相同的四分之一圆的草坪,若圆形草坪的半径为r,长方形的长为a,宽为b,请用整式表示空地的面积,并指出这个整式是单项式还是多项式.若是单项式,指出它的系数;若是多项式,指出它有几项,各项的系数分别是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们知道:x2-6x=(x2-6x+9)-9=(x-3)2-9;-x2+10=-(x2-10x+25)+25=-(x-5)2+25,这一种方法称为配方法,利用配方法请解以下各题:
我们知道:x2-6x=(x2-6x+9)-9=(x-3)2-9;-x2+10=-(x2-10x+25)+25=-(x-5)2+25,这一种方法称为配方法,利用配方法请解以下各题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com