
【题目】如图1,抛物线y=ax2+2ax+c(a≠0)与x轴交于点A,B(1,0)两点,与y轴交于点C,且OA=OC.
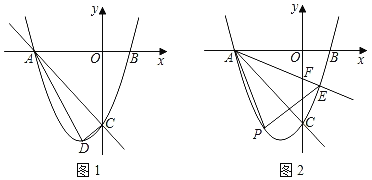
(1)求抛物线的解析式;
(2)点D是抛物线顶点,求△ACD的面积;
(3)如图2,射线AE交抛物线于点E,交y轴的负半轴于点F(点F在线段AE上),点P是直线AE下方抛物线上的一点,S△ABE=![]() ,求△APE面积的最大值和此动点P的坐标.
,求△APE面积的最大值和此动点P的坐标.
【答案】(1)y=x2+2x﹣3;(2)3;(3)P的坐标为(﹣![]() ,﹣
,﹣![]() )
)
【解析】
(1)先求出点C的坐标,再根据待定系数法即可得出答案;
(2)根据(1)中求出的函数解析式得出点A、C和D的坐标,再利用割补法即可得出答案;
(3)设点E的纵坐标为t,根据△ABE的面积求出t的值,再代入函数解析式即可得出点E的坐标,将A和E的坐标代入即可得出直线AE的解析式,接着根据S△APE=S△APG+S△PEG求出面积的函数关系式,再化为顶点式即可得出答案.
解:(1)∵抛物线y=ax2+2ax+c(a≠0)与x轴交于点A,B(1,0)两点,与y轴交于点C,且OA=OC,
∴a+2a+c=0,点C的坐标为(0,c),
∴点A的坐标为(c,0),
∴ac2+2ac+c=0,
∴![]() ,
,
解得,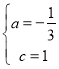 或
或![]() ,
,
∵函数图象开口向上,
∴a>0,
∴a=1,c=﹣3,
∴抛物线的解析式为y=x2+2x﹣3;
(2)∵y=x2+2x﹣3=(x+1)2﹣4,抛物线与与y轴交于点C,顶点为D,OA=OC,抛物线y=ax2+2ax+c(a≠0)与x轴交于点A,B(1,0)两点,
∴点D的坐标为(﹣1,﹣4),点C的坐标为(0,﹣3),点A的坐标为(﹣3,0),
连接OD,如右图1所示,
由图可知:
S△ACD=S△OAD+S△OCD﹣S△OAC
=![]()
=3;
(3)∵A(﹣3,0),点B(1,0),
∴AB=4,
设点E的纵坐标为t,t<0,
∵S△ABE=![]() ,
,
∴![]() ,得t=
,得t=![]() ,
,
把y=![]() 代入y=x2+2x﹣3,得
代入y=x2+2x﹣3,得
![]() =x2+2x﹣3,
=x2+2x﹣3,
解得,x1=![]() ,x2=
,x2=![]() ,
,
∵点E在y轴的右侧,
∴点E(![]() ,
,![]() ),
),
设直线AE的解析式为y=mx+n(m≠0),
∴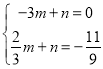 ,得
,得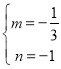 ,
,
∴直线AE的解析式为y=![]() x﹣1,
x﹣1,
过点P作y轴的平行线交AC于点G,如图2所示,
设点P的横坐标为x,则P(x,x2+2x﹣3),点G(x,![]() x﹣1),
x﹣1),
∴PG=(![]() x﹣1)﹣(x2+2x﹣3)=﹣x2﹣
x﹣1)﹣(x2+2x﹣3)=﹣x2﹣![]() x+2,
x+2,
又∵A(﹣3,0),E(![]() ,
,![]() ),
),
∴S△APE=S△APG+S△PEG
=![]()
=![]()
=![]() ,
,
∴当x=﹣![]() 时,S△APE取得最大值,最大值是
时,S△APE取得最大值,最大值是![]() ,
,
把x=﹣![]() 代入y=x2+2x﹣3,得
代入y=x2+2x﹣3,得
y=(﹣![]() )2+2×(﹣
)2+2×(﹣![]() )﹣3=﹣
)﹣3=﹣![]() ,
,
∴此时点P的坐标为(﹣![]() ,﹣
,﹣![]() ).
).




科目:初中数学 来源: 题型:
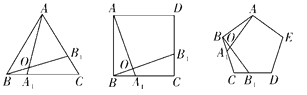
【题目】如图,下列正多边形都满足BA1=CB1,在正三角形中,我们可推得:∠AOB1=60°;在正方形中,可推得:∠AOB1=90°;在正五边形中,可推得:∠AOB1=108°,依此类推在正八边形中,AOB1=____°,在正n(n≥3)边形中,∠AOB1=____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列内容,并解决问题.
一道习题引发的思考
小明在学习《勾股定理》一章内容时,遇到了一个习题,并对有关内容进行了研究;
习题再现:
古希腊的哲学家柏拉图曾指出,如果![]() 表示大于1的整数,
表示大于1的整数,![]() ,
,![]() ,
,![]() ,那么
,那么![]() ,
,![]() ,
,![]() 为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
资料搜集:
定义:勾股数是指可以构成一个直角三角形三边的一组正整数.一般地,若三角形三边长![]() ,
,![]() ,
,![]() 都是正整数,且满足
都是正整数,且满足![]() ,那么
,那么![]() ,
,![]() ,
,![]() 称为一组勾股数.
称为一组勾股数.
关于勾股数的研究:我囯西周初数学家商高在公元前1000年发现了“勾三,股四,弦五”,这组数![]() 是世界上最早发现的一组勾股效,毕达哥拉斯学派、柏拉图学派、我国数学家刘徽、古希腊数学家丢番图都进行过勾股数的研究.习题中的表达式是柏拉图给出的勾股数公式,这个表达式未给出全部勾股数,世界上第一次给出勾股数通解公式的是《九幸算术),其勾股数公式为:
是世界上最早发现的一组勾股效,毕达哥拉斯学派、柏拉图学派、我国数学家刘徽、古希腊数学家丢番图都进行过勾股数的研究.习题中的表达式是柏拉图给出的勾股数公式,这个表达式未给出全部勾股数,世界上第一次给出勾股数通解公式的是《九幸算术),其勾股数公式为:![]() ,
,![]() ,
,![]()
![]() ,其中
,其中![]() ,
,![]() ,
,![]() 是互质的奇数.(注:
是互质的奇数.(注:![]() ,
,![]() ,
,![]() 的相同倍数组成的一组数也是勾股数)
的相同倍数组成的一组数也是勾股数)

问题解答:
(1)根据柏拉图的研究,当![]() 时,请直接写出一组勾股数;
时,请直接写出一组勾股数;
(2)若![]() 表示大于1的整数,试证明
表示大于1的整数,试证明![]() 是一组勾股数;
是一组勾股数;
(3)请举出一个反例(即写出一组勾股数),说明柏拉图给出的勾股数公式不能构造出所有的勾股数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承接了60万平方米的绿化工程,由于情况有变,…设原计划每天绿化的面积为![]() 万平方米,列方程为
万平方米,列方程为![]() ,根据方程可知省路的部分是( )
,根据方程可知省路的部分是( )
A.实际每天的工作效率比原计划提高了![]() ,结果提前30天完成了这一任务
,结果提前30天完成了这一任务
B.实际每天的工作效率比原计划提高了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
C.实际每天的工作效率比原计划降低了![]() ,结果延误30天完成了这一任务
,结果延误30天完成了这一任务
D.实际每天的工作效率比原计划降低了![]() ,结果提前30天完成了这一任务
,结果提前30天完成了这一任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() 和点
和点![]() ,点
,点![]() 在点
在点![]() 的右侧,点
的右侧,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 沿
沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位后得到线段
个单位后得到线段![]() .
.
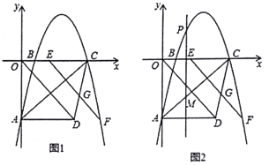
(1)当![]() ______时,点
______时,点![]() 或点
或点![]() 正好移动到抛物线上;
正好移动到抛物线上;
(2)当点![]() 正好移动到抛物线上,
正好移动到抛物线上,![]() 与
与![]() 相交于点
相交于点![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)如图2,若点![]() 是
是![]() 轴上方抛物线上一动点,过点
轴上方抛物线上一动点,过点![]() 作平行于
作平行于![]() 轴的直线交
轴的直线交![]() 于点
于点![]() ,探索是否存在点
,探索是否存在点![]() ,使线段
,使线段![]() 长度有最大值?若存在,直接写出点
长度有最大值?若存在,直接写出点![]() 的坐标和
的坐标和![]() 长度的最大值;若不存在,请说明理由.
长度的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
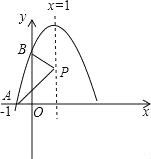
【题目】已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x,y轴的交点分别为A,B,P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0,②x=3是ax2+bx+3=0的一个根,③△PAB周长的最小值是![]() +3
+3![]() .其中正确的是( )
.其中正确的是( )
A. ①②③ B. 仅有①② C. 仅有①③ D. 仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形![]() 的顶点
的顶点![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() 于点
于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,连接
,连接![]() .
.
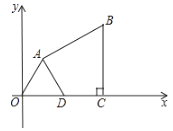
(1)求证:![]() 是等边三角形;
是等边三角形;
(2)求点![]() 的坐标;
的坐标;
(3)平行于![]() 的直线
的直线![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴正方向平移.设直线
轴正方向平移.设直线![]() 被四边形
被四边形![]() 截得的线段长为
截得的线段长为![]() ,直线
,直线![]() 与
与![]() 轴交点的横坐标为
轴交点的横坐标为![]() .
.
①当直线![]() 与
与![]() 轴的交点在线段
轴的交点在线段![]() 上(交点不与点
上(交点不与点![]() 重合)时,请直接写出
重合)时,请直接写出![]() 与
与![]() 的函数关系式(不必写出自变量
的函数关系式(不必写出自变量![]() 的取值范围)
的取值范围)
②若![]() ,请直接写出此时直线
,请直接写出此时直线![]() 与
与![]() 轴的交点坐标.
轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,BC=6,DE是△ABC的中位线,点D在AB上,把点B绕点D按顺时针方向旋转α(0°<α<180°)角得到点F,连接AF,BF.下列结论:①△ABF是直角三角形;②若△ABF和△ABC全等,则α=2∠BAC或2∠ABC;③若α=90°,连接EF,则S△DEF=4.5;其中正确的结论是( )
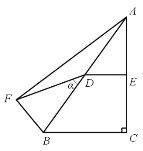
A.①②B.①③C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
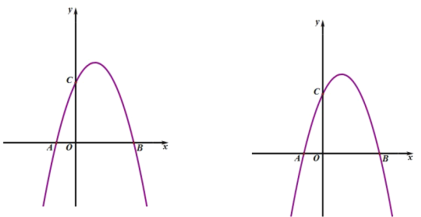
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点
若点![]() 为第一象限抛物线上一点,连接
为第一象限抛物线上一点,连接![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() 连接
连接![]() 过点
过点![]() 作直线
作直线![]() 的垂线,垂足为点E,过点
的垂线,垂足为点E,过点![]() 作直线
作直线![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,作线段
,作线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 在
在![]() 的条件下,延长
的条件下,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 的正切值.
的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com