
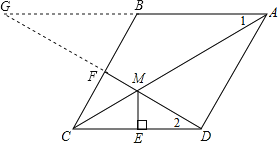
【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

【答案】(1)解:∵四边形ABCD是菱形,
∴AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠ACD=∠2,
∴MC=MD,
∵ME⊥CD,
∴CD=2CE,
∵CE=1,
∴CD=2,
∴BC=CD=2;
(2)证明:如图,∵F为边BC的中点,
∴BF=CF=![]() BC,
BC,
∴CF=CE,
在菱形ABCD中,AC平分∠BCD,
∴∠ACB=∠ACD,
在△CEM和△CFM中,
∵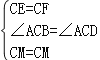 ,
,
∴△CEM≌△CFM(SAS),
∴ME=MF,
延长AB交DF于点G,
∵AB∥CD,
∴∠G=∠2,
∵∠1=∠2,
∴∠1=∠G,
∴AM=MG,
在△CDF和△BGF中,
∵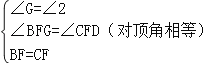 ,
,
∴△CDF≌△BGF(AAS),
∴GF=DF,
由图形可知,GM=GF+MF,
∴AM=DF+ME.
【解析】(1)根据菱形的对边平行可得AB∥D,再根据两直线平行,内错角相等可得∠1=∠ACD,所以∠ACD=∠2,根据等角对等边的性质可得CM=DM,再根据等腰三角形三线合一的性质可得CE=DE,然后求出CD的长度,即为菱形的边长BC的长度;
(2)先利用“边角边”证明△CEM和△CFM全等,根据全等三角形对应边相等可得ME=MF,延长AB交DF于点G,然后证明∠1=∠G,根据等角对等边的性质可得AM=GM,再利用“角角边”证明△CDF和△BGF全等,根据全等三角形对应边相等可得GF=DF,最后结合图形GM=GF+MF即可得证.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】学校开展综合实践活动中,某班进行了小制作评比,作品上交时间为5月11日至5月30日,评委们把同学们上交作品的件数按5天一组分组统计,绘制了频数分布直方图如下,小长方形的高之比为:2:5:2:1.现已知第二组的上交作品件数是20件.求:

(1)此班这次上交作品共 件;
(2)评委们一致认为第四组的作品质量都比较高,现从中随机抽取2件作品参加学校评比,小明的两件作品都在第四组中,他的两件作品都被抽中的概率是多少?(请写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与x轴交于点A,与y轴交于点B.点C是x轴上一动点,点D为(3,0),抛物线
与x轴交于点A,与y轴交于点B.点C是x轴上一动点,点D为(3,0),抛物线![]() 过B、C、D三点.
过B、C、D三点.
(1)如图1所示,若点C与点A关于y轴对称.
①求直线BD和抛物线的解析式;
②若点P是抛物线对称轴上一动点,当BP+CP的值最小时,求点P的坐标;
③若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标;
(2)如图2,若BE//x轴,且E(4,3),点A1与点A关于直线BC对称,当EA1的长最小时,直接写出OC的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]() 的解满足x<0,y>0.
的解满足x<0,y>0.
(1)x=________, y=________(用含a的代数式表示);
(2)求a的取值范围;
(3)若2x8y=2m,用含有a的代数式表示m,并求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中,△ABC不是直角三角形的是 ( )
A. b2=a2-c2 B. ∠A:∠B:∠C=3:4:5
C. ∠C=∠A-∠B D. a2:b2:c2=1:3:2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com