
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬øų³öČēĻĀ¶ØŅå:ŅŃÖŖĮ½øöŗÆŹż£¬Čē¹ū¶ŌÓŚČĪŅāµÄ×Ō±äĮæ![]() ,ÕāĮ½øöŗÆŹż¶ŌÓ¦µÄŗÆŹżÖµ¼ĒĪŖ
,ÕāĮ½øöŗÆŹż¶ŌÓ¦µÄŗÆŹżÖµ¼ĒĪŖ![]() , ŗćÓŠµć
, ŗćÓŠµć![]() ŗĶµć
ŗĶµć![]() ¹ŲÓŚµć
¹ŲÓŚµć![]() ³ÉÖŠŠÄ¶Ō³Ę(“ĖČżøöµćæÉŅŌÖŲŗĻ)£¬ÓÉÓŚ¶Ō³ĘÖŠŠÄ
³ÉÖŠŠÄ¶Ō³Ę(“ĖČżøöµćæÉŅŌÖŲŗĻ)£¬ÓÉÓŚ¶Ō³ĘÖŠŠÄ![]() ¶¼ŌŚÖ±Ļß
¶¼ŌŚÖ±Ļß![]() ÉĻ£¬ĖłŅŌ³ĘÕāĮ½øöŗÆŹżĪŖ¹ŲÓŚÖ±Ļß
ÉĻ£¬ĖłŅŌ³ĘÕāĮ½øöŗÆŹżĪŖ¹ŲÓŚÖ±Ļß![]() µÄ”°ĻąŅĄŗÆŹż”±”£ĄżČē:
µÄ”°ĻąŅĄŗÆŹż”±”£ĄżČē: ![]() ŗĶ
ŗĶ![]() ĪŖ¹ŲÓŚÖ±Ļß
ĪŖ¹ŲÓŚÖ±Ļß![]() µÄ ”°ĻąŅĄŗÆŹż”±.
µÄ ”°ĻąŅĄŗÆŹż”±.
£Ø1£©ŅŃÖŖµć![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ÉĻŅ»µć£¬ĒėĒó³öµć
ÉĻŅ»µć£¬ĒėĒó³öµć![]() ¹ŲÓŚµć
¹ŲÓŚµć![]() ³ÉÖŠŠÄ¶Ō³ĘµÄµć
³ÉÖŠŠÄ¶Ō³ĘµÄµć![]() µÄ×ų±ź:
µÄ×ų±ź:
£Ø2£©ČōÖ±Ļß![]() ŗĶĖü¹ŲÓŚÖ±Ļß
ŗĶĖü¹ŲÓŚÖ±Ļß![]() µÄ”°ĻąŅĄŗÆŹż”±µÄĶ¼ĻóÓė
µÄ”°ĻąŅĄŗÆŹż”±µÄĶ¼ĻóÓė![]() ÖįĪ§³ÉµÄČż½ĒŠĪµÄĆ껿ĪŖ
ÖįĪ§³ÉµÄČż½ĒŠĪµÄĆ껿ĪŖ![]() £¬Ēó
£¬Ēó![]() µÄÖµ;
µÄÖµ;
£Ø3£©Čō¶ž“ĪŗÆŹż![]() ŗĶ
ŗĶ![]() ĪŖ¹ŲÓŚÖ±Ļß
ĪŖ¹ŲÓŚÖ±Ļß![]() µÄ”°ĻąŅĄŗÆŹż”±.
µÄ”°ĻąŅĄŗÆŹż”±.
¢ŁĒėĒó³ö![]() µÄÖµ;
µÄÖµ;
¢ŚŅŃÖŖµć![]() ”¢µć
”¢µć![]() Į¬½Ó
Į¬½Ó![]() Ö±½ÓŠ“³ö
Ö±½ÓŠ“³ö![]() ŗĶ
ŗĶ![]() Į½ĢõÅ×ĪļĻßÓėĻ߶Ī
Į½ĢõÅ×ĪļĻßÓėĻ߶Ī![]() ÓŠÄæÖ»ÓŠĮ½øö½»Õ¼Ź±¶ŌÓ¦µÄ
ÓŠÄæÖ»ÓŠĮ½øö½»Õ¼Ź±¶ŌÓ¦µÄ![]() µÄȔֵ·¶Ī§.
µÄȔֵ·¶Ī§.
”¾“š°ø”æ£Ø1£©£Ø1£¬-4£©£»£Ø2£©![]() £»£Ø3£©¢Ł-1£¬2 £» ¢Ś
£»£Ø3£©¢Ł-1£¬2 £» ¢Ś![]() »ņ
»ņ![]()
”¾½āĪö”æ
£Ø1£©ĻČĒó³öµćMµÄ×ų±ź£¬øł¾ŻµćMÓėµćN¹ŲÓŚ![]() ³ÉÖŠŠÄ¶Ō³Ę£¬¼“æÉĒó³öµćNµÄ×ų±ź£»
³ÉÖŠŠÄ¶Ō³Ę£¬¼“æÉĒó³öµćNµÄ×ų±ź£»
£Ø2£©Éčµć![]() ŗĶµć
ŗĶµć![]() ·Ö±šŹĒÖ±Ļß
·Ö±šŹĒÖ±Ļß![]() ÓėĖüµÄ”°ĻąŅĄŗÆŹż”±µÄĶ¼ĻóÉĻµÄČĪŅāŅ»µć£¬øł¾ŻĻąŅĄŗÆŹżµÄ¶ØŅ壬æÉµĆ£ŗÖ±Ļß
ÓėĖüµÄ”°ĻąŅĄŗÆŹż”±µÄĶ¼ĻóÉĻµÄČĪŅāŅ»µć£¬øł¾ŻĻąŅĄŗÆŹżµÄ¶ØŅ壬æÉµĆ£ŗÖ±Ļß![]() ¹ŲÓŚÖ±Ļßy=xµÄĻąŅĄŗÆŹżŹĒ£ŗ
¹ŲÓŚÖ±Ļßy=xµÄĻąŅĄŗÆŹżŹĒ£ŗ![]() £¬½įŗĻ”°Ö±Ļß
£¬½įŗĻ”°Ö±Ļß![]() ŗĶĖü¹ŲÓŚÖ±Ļß
ŗĶĖü¹ŲÓŚÖ±Ļß![]() µÄ”°ĻąŅĄŗÆŹż”±µÄĶ¼ĻóÓė
µÄ”°ĻąŅĄŗÆŹż”±µÄĶ¼ĻóÓė![]() ÖįĪ§³ÉµÄČż½ĒŠĪµÄĆ껿ĪŖ
ÖįĪ§³ÉµÄČż½ĒŠĪµÄĆ껿ĪŖ![]() ”±£¬ĮŠ³ö¹ŲÓŚnµÄ·½³Ģ£¬¼“æÉĒó½ā£»
”±£¬ĮŠ³ö¹ŲÓŚnµÄ·½³Ģ£¬¼“æÉĒó½ā£»
£Ø3£©¢ŁÓÉĻąŅĄŗÆŹżµÄ¶ØŅ壬µĆ£ŗ![]() £¬»Æ¼ņÕūĄķŗ󣬼“æÉĒó½ā£»¢Ś·ÖĖÄÖÖĒéæö»³ö¶ž“ĪŗÆŹż
£¬»Æ¼ņÕūĄķŗ󣬼“æÉĒó½ā£»¢Ś·ÖĖÄÖÖĒéæö»³ö¶ž“ĪŗÆŹż![]() £¬
£¬![]() µÄĶ¼Ļ󣬼“æɵƵ½“š°ø£®
µÄĶ¼Ļ󣬼“æɵƵ½“š°ø£®
£Ø1£©”ßµć![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ÉĻŅ»µć£¬
ÉĻŅ»µć£¬
”ą![]() £¬¼“£ŗ
£¬¼“£ŗ![]() £¬
£¬
”ßµćNÓėµć![]() ¹ŲÓŚ
¹ŲÓŚ![]() ³ÉÖŠŠÄ¶Ō³Ę£¬
³ÉÖŠŠÄ¶Ō³Ę£¬
”ą![]() £»
£»
£Ø2£©Éčµć![]() ŗĶµć
ŗĶµć![]() ·Ö±šŹĒÖ±Ļß
·Ö±šŹĒÖ±Ļß![]() ÓėĖüµÄ”°ĻąŅĄŗÆŹż”±µÄĶ¼ĻóÉĻµÄČĪŅāŅ»µć£¬
ÓėĖüµÄ”°ĻąŅĄŗÆŹż”±µÄĶ¼ĻóÉĻµÄČĪŅāŅ»µć£¬
”ą![]() £¬
£¬
![]() £¬
£¬
”ąÖ±Ļß![]() ¹ŲÓŚÖ±Ļßy=xµÄĻąŅĄŗÆŹżŹĒ£ŗ
¹ŲÓŚÖ±Ļßy=xµÄĻąŅĄŗÆŹżŹĒ£ŗ![]() £¬
£¬
ĮŖĮ¢![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £¬
£¬
”ąÖ±Ļß![]() ÓėÖ±Ļß
ÓėÖ±Ļß![]() µÄ½»µćµÄŗį×ų±źĪŖ
µÄ½»µćµÄŗį×ų±źĪŖ![]() £¬
£¬
”ßÖ±Ļß![]() ÓėÖ±Ļß
ÓėÖ±Ļß![]() ÓėyÖįµÄ½»µć×ų±ź·Ö±šŹĒ£ŗ(0£¬n)£¬(0£¬-n)£¬
ÓėyÖįµÄ½»µć×ų±ź·Ö±šŹĒ£ŗ(0£¬n)£¬(0£¬-n)£¬
ÓÉĢāŅāµĆ£ŗ![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £»
£»
£Ø3£©¢ŁÓÉĢāŅāµĆ£ŗ![]() £¬
£¬
”ą![]() £¬¶ŌÓŚČĪŅāµÄx¶¼³ÉĮ¢£¬
£¬¶ŌÓŚČĪŅāµÄx¶¼³ÉĮ¢£¬
”ą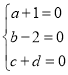 £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £»
£»
¢ŚÓɵŚ¢ŁŠ”Ģā£¬æÉÖŖ£ŗ![]() £¬
£¬![]() £¬
£¬
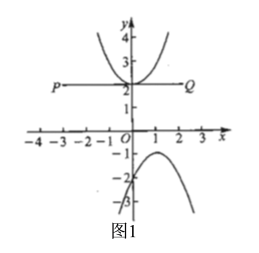
µ±![]() Ź±£¬ČēĶ¼1£¬
Ź±£¬ČēĶ¼1£¬
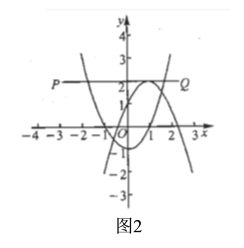
µ±![]() Ź±£¬ČēĶ¼2£¬
Ź±£¬ČēĶ¼2£¬
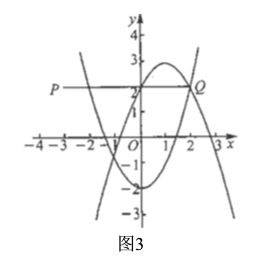
µ±![]() Ź±£¬ČēĶ¼3£¬
Ź±£¬ČēĶ¼3£¬
µ±![]() Ź±£¬ČēĶ¼4£¬
Ź±£¬ČēĶ¼4£¬
×ŪÉĻæÉÖŖ:![]() »ņ
»ņ![]() Ź±£¬Å×ĪļĻßÓėĻ߶Ī
Ź±£¬Å×ĪļĻßÓėĻ߶Ī![]() ÓŠĒŅÖ»ÓŠĮ½øö½»µć£®
ÓŠĒŅÖ»ÓŠĮ½øö½»µć£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
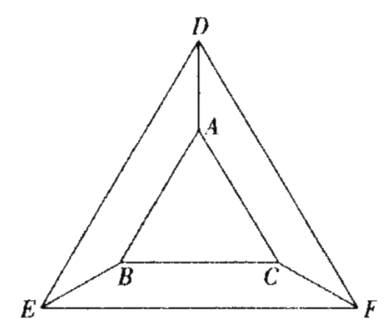
”¾ĢāÄæ”æČēĶ¼£¬“ӵȱߔ÷ABCµÄČżøö¶„µć³ö·¢£¬ĻņĶā·Ö±šŅż“¹Ö±ÓŚ¶Ō±ßµÄÉäĻߣ¬ŌŚÉäĻßÉĻ·Ö±š½ŲČ”![]() £¬Čō
£¬Čō![]() £¬ŌņµČ±ß
£¬ŌņµČ±ß![]() µÄ±ß³¤ĪŖ( )
µÄ±ß³¤ĪŖ( )
A.2B.3C.![]() D.6
D.6
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖCĪŖĻ߶ĪABÖŠµć£¬”ĻACM£½¦Į£®QĪŖĻ߶ĪBCÉĻŅ»¶Æµć£Ø²»ÓėµćBÖŲŗĻ£©£¬µćPŌŚÉäĻßCMÉĻ£¬Į¬½ÓPA£¬PQ£¬¼ĒBQ£½kCP£®
£Ø1£©Čō¦Į£½60”ć£¬k£½1£¬
¢ŁČēĶ¼1£¬µ±QĪŖBCÖŠµćŹ±£¬Ēó”ĻPACµÄ¶ČŹż£»
¢ŚÖ±½ÓŠ“³öPA”¢PQµÄŹżĮæ¹ŲĻµ£»
£Ø2£©ČēĶ¼2£¬µ±¦Į£½45”揱£®Ģ½¾æŹĒ·ń“ęŌŚ³£Źżk£¬Ź¹µĆ¢ŚÖŠµÄ½įĀŪČŌ³ÉĮ¢£æČō“ęŌŚ£¬Š“³ökµÄÖµ²¢Ö¤Ć÷£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŅĆĒÖŖµĄ£¬£Øk+1£©2£½k2+2k+1£¬±äŠĪµĆ£ŗ£Øk+1£©2©k2£½2k+1£¬¶ŌÉĻĆęµÄµČŹ½£¬ŅĄ“ĪĮīk£½1£¬2£¬3£¬”µĆ£ŗ
µŚ1øöµČŹ½£ŗ22©12£½2”Į1+1
µŚ2øöµČŹ½£ŗ32©22£½2”Į2+1
µŚ3øöµČŹ½£ŗ42©32£½2”Į3+1
£Ø1£©°“¹ęĀÉ£¬Š“³öµŚnøöµČŹ½£ØÓĆŗ¬nµÄµČŹ½±ķŹ¾£©£ŗµŚnøöµČŹ½”” ””£®
£Ø2£©¼ĒS1£½1+2+3+”+n£¬½«ÕānøöµČŹ½Į½±ß·Ö±šĻą¼Ó£¬ÄćÄÜĒó³öS1µÄ¹«Ź½Āš£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾µÄÅ×ĪļĻ߶Ō³ĘÖįŹĒÖ±Ļßx£½1£¬ÓėxÖįÓŠĮ½øö½»µć£¬ÓėyÖį½»µć×ų±źŹĒ£Ø0£¬3£©£¬°ŃĖüĻņĻĀĘ½ŅĘ2øöµ„Ī»ŗó£¬µĆµ½ŠĀµÄÅ×ĪļĻß½āĪöŹ½ŹĒ y£½ax2+bx+c£¬ŅŌĻĀĖÄøö½įĀŪ£ŗ¢Łb2©4ac£¼0£¬¢Śabc£¼0£¬¢Ū4a+2b+c£½1£¬¢Üa©b+c£¾0ÖŠ£¬ÅŠ¶ĻÕżČ·µÄÓŠ£Ø””””£©
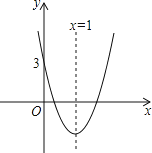
A. ¢Ś¢Ū¢ÜB. ¢Ł¢Ś¢ŪC. ¢Ś¢ŪD. ¢Ł¢Ü
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”澩ŗ¼“óŌĖŗÓŹĒŹĄ½ēĪÄ»ÆŅŲś£®×ŪŗĻŹµ¼ł»ī¶ÆŠ”×éĪŖĮĖ²ā³öij¶ĪŌĖŗÓµÄŗÓæķ£Ø°¶ŃŲŹĒĘ½ŠŠµÄ£©£¬ČēĶ¼£¬ŌŚ°¶±ß·Ö±šŃ”¶ØĮĖµćA”¢BŗĶµćC”¢D£¬ĻČÓĆ¾ķ³ßĮæµĆAB=160m£¬CD=40m£¬ŌŁÓĆ²ā½ĒŅĒ²āµĆ”ĻCAB=30”ć£¬”ĻDBA=60”ć£¬ĒóøƶĪŌĖŗÓµÄŗÓæķ£Ø¼“CHµÄ³¤£©£®
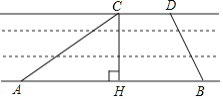
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
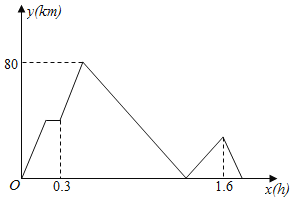
”¾ĢāÄæ”æA£¬BĮ½Õ¾Ļą¾ą330Ē§Ć×£¬¼×”¢ŅŅĮ½³µ¶¼“ÓAÕ¾³ö·¢æŖĶłBÕ¾£¬¼×³µĻČ³ö·¢£¬ĒŅŌŚĶ¾ÖŠCÕ¾Ķ£ææ6·ÖÖÓ£¬¼×³µ³ö·¢°ėŠ”Ź±ŗó£¬ŅŅ³µ“ÓAÕ¾Ö±“ļBÕ¾ŗóĶ£Ö¹£¬Į½³µÖ®¼äµÄ¾ąĄėy£ØĒ§Ć×£©Óė¼×³µŠŠŹ»µÄŹ±¼äx£ØŠ”Ź±£©Ö®¼äµÄŗÆŹżĶ¼ĻóČēĶ¼£¬ŌņŅŅ³µĒ”ŗĆ×·ÉĻ¼×³µŹ±¾ąĄėCÕ¾ÓŠ______Ē§Ć×£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
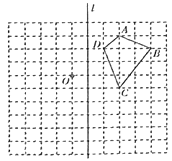
”¾ĢāÄæ”æČēĶ¼ŌŚ±ß³¤ĪŖ1øöµ„Ī»³¤¶ČµÄŠ”Õż·½ŠĪ×é³ÉµÄĶųøńÖŠ£¬øų³öĮĖøńµćĖıߊĪ![]() £Ø¶„µćŹĒĶųøńĻߵĽ»µć£©£®
£Ø¶„µćŹĒĶųøńĻߵĽ»µć£©£®
£Ø1£©Ēė»³öĖıߊĪ![]() ¹ŲÓŚÖ±Ļß
¹ŲÓŚÖ±Ļß![]() ¶Ō³ĘµÄĖıߊĪ
¶Ō³ĘµÄĖıߊĪ![]() £Øµć
£Øµć![]() µÄ¶ŌÓ¦µć·Ö±šĪŖµć
µÄ¶ŌÓ¦µć·Ö±šĪŖµć![]() £©£»
£©£»
£Ø2£©ČōŅŌµć![]() ĪŖĪ»ĖĘÖŠŠÄ£¬½«ĖıߊĪ
ĪŖĪ»ĖĘÖŠŠÄ£¬½«ĖıߊĪ![]() ·Å“óµ½ŌĄ“µÄ2±¶£¬ĒėŌŚøĆĶųøńÖŠ»³ö·Å“óŗóµÄĖıߊĪ
·Å“óµ½ŌĄ“µÄ2±¶£¬ĒėŌŚøĆĶųøńÖŠ»³ö·Å“óŗóµÄĖıߊĪ![]() £Øµć
£Øµć![]() µÄ¶ŌÓ¦µć·Ö±šĪŖµć
µÄ¶ŌÓ¦µć·Ö±šĪŖµć![]() £©£»
£©£»
£Ø3£©ĢīæÕ£ŗ![]() __________£®
__________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
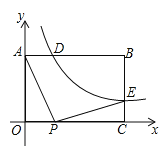
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬·“±ČĄżŗÆŹż
£¬·“±ČĄżŗÆŹż![]() £Ø
£Ø![]() £©µÄĶ¼ĻńÓė¾ŲŠĪĮ½±ßAB”¢BC·Ö±š½»ÓŚµćD”¢µćE£¬ĒŅ
£©µÄĶ¼ĻńÓė¾ŲŠĪĮ½±ßAB”¢BC·Ö±š½»ÓŚµćD”¢µćE£¬ĒŅ![]() .
.
£Ø1£©ĒóµćDµÄ×ų±źŗĶ![]() µÄÖµ£»
掙术
£Ø2£©ĒóÖ¤£ŗ![]() £»
£»
£Ø3£©Čōµć![]() ŹĒĻ߶Ī
ŹĒĻ߶Ī![]() ÉĻµÄŅ»øö¶Æµć£¬ŹĒ·ń“ęŌŚµć
ÉĻµÄŅ»øö¶Æµć£¬ŹĒ·ń“ęŌŚµć![]() £¬Ź¹
£¬Ź¹![]() £æČō“ęŌŚ£¬Ēó³ö“ĖŹ±µć
£æČō“ęŌŚ£¬Ēó³ö“ĖŹ±µć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com