
【题目】如图,![]() 逆时针旋转到
逆时针旋转到![]() ,其中
,其中![]() ,点
,点![]() 在同-直线上.
在同-直线上.

(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)指出对应线段、对应角及对应点.
【答案】![]() 旋转中心
旋转中心![]() 点;
点;![]() 转
转![]() ;
;![]() 详见解析.
详见解析.
【解析】
(1)△AOC经过旋转得到△BOD,旋转中心为点O;(2)线段OA的对应线段为OB,旋转角为∠AOB.根据已知条件即可求出旋转度数;(3)根据旋转中心,即可确定对应线段、对应角及对应点.
(1)依题意,△AOC经过旋转得到△BOD,
所以旋转中心为点O,
(2)因为∠BOD=∠AOC,∠AOC=120°,点A、O、D在同一直线上.
所以∠AOB=180°-120°=60°.
因为线段OB的对应线段为OA,
所以旋转角为∠AOB=60°
(3)对应角:∠A对应∠ OBD; ∠C对应∠D; ∠AOC对应∠ BOD;
对应线段:OA对应OB;OC对应OD;CA对应DB;
对应点:A对应 B; C对应D.


科目:初中数学 来源: 题型:
【题目】某学校为了推动球类运动的普及,成立多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题:

(1)本次抽样调查,共调查了 名学生;
(2)请将条形统计图和扇形统计图补充完整;
(3)若该学校共有学生1800人,根据以上数据分析,试估计选择排球运动的同学约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今,青少年用电脑手机过多,视力水平下降已引起了全社会的关注,某校为了解八年级1000名学生的视力情况,从中抽查了150名学生的视力情况,通过数据处理,得到如下的频数分布表.解答下列问题:
视力范围分组 | 组中值 | 频数 |
3.95≤x<4.25 | 4.1 | 20 |
4.25≤x<4.55 | 4.4 | 10 |
4.55≤x<4.85 | 4.7 | 30 |
4.85≤x<5.15 | 5.0 | 60 |
5.15≤x<5.45 | 5.3 | 30 |
合计 | 150 |
(1)分别指出参加抽测学生的视力的众数、中位数所在的范围;
(2)若视力为4.85以上(含4.85)为正常,试估计该校八年级学生视力正常的人数约为多少?
(3)根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数相应组中的权.请你估计该校八年级学生的平均视力是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮与小明做投骰子(质地均匀的正方体)的实验与游戏.
(1)在实验中他们共做了50次试验,试验结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 10 | 9 | 6 | 9 | 8 | 8 |
填空:此次实验中,“1点朝上”的频率是 ;
② 小亮说:“根据试验,出现1点朝上的概率最大.”他的说法正确吗?为什么?
(2)小明也做了大量的同一试验,并统计了“1点朝上”的次数,获得的数据如下表:
试验总次数 | 100 | 200 | 500 | 1000 | 2000 | 5000 | 10000 |
1点朝上的次数 | 18 | 34 | 82 | 168 | 330 | 835 | 1660 |
1点朝上的频率 | 0.180 | 0.170 | 0.164 | 0.168 | 0.165 | 0.167 | 0.166 |
“1点朝上”的概率的估计值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐锐参加我市电视台组织的“牡丹杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,这两道题锐锐都不会,不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
(1)如果锐锐两次“求助”都在第一道题中使用,那么锐锐通关的概率是________;
(2)如果锐锐两次“求助”都在第二道题中使用,那么锐锐通关的概率是________;
(3)如果锐锐每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B,C三点在同一条数轴上.
(1)、若点A,B表示的数分别为-4,2,且BC=![]() AB,则点C表示的数是 ;
AB,则点C表示的数是 ;
(2)、点A,B表示的数分别为m,n,且m<n.
①若AC-AB=2,求点C表示的数(用含m,n的式子表示);
②点D是这条数轴上的一个动点,且点D在点A的右侧(不与点B重合),当AD=2AC,BC=![]() BD,求线段AD的长(用含m,n的式子表示).
BD,求线段AD的长(用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
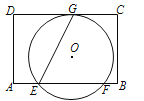
【题目】如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=![]() AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=
AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=![]() .当边AD或BC所在的直线与⊙O相切时,AB的长是 .
.当边AD或BC所在的直线与⊙O相切时,AB的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了“求简单随机事件发生的可能性大小”知识后,小敏,小聪,小丽三人分别编写了一道有关随机事件的试题并进行了解答.小敏,小聪,小丽编写的试题分别是下面的(1)(2)(3).
(1)一个不透明的盒子里装有4个红球,2个白球,除颜色外其它都相同,搅均后,从中随意摸出一个球,摸出红球的可能性是多少?解:P(摸出一个红球)=![]() .
.
(2)口袋里装有如图所示的1角硬币2枚、5角硬币2枚、1 元硬币1枚.搅均后,从中随意摸出一枚硬币,摸出1角硬币的可能性是多少?解:P(摸出1角的硬币)=![]() .
.
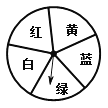
(3)如图,是一个转盘,盘面上有5个全等的扇形区域,每个区域显示有不同的颜色,轻轻转动转盘,当转盘停止后,指针对准红色区域的可能性是多少?解:P(指针对准红色区域)=![]() .
.
问题:根据以上材料回答问题:小敏,小聪,小丽三人中,谁编写的试题及解答是正确的,并简要说明其他两人所编试题或解答的不足之处.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com