
分析 (1)可设这个外角的度数是x°,根据等量关系:一个内角相邻的外角与其他各内角的和为600°,列出方程求解即可;
(2)设边数为n,这个外角的度数是x°,根据等量关系:一个内角相邻的外角与其他各内角的和为600°,列出方程,再根据0<x<180,即0<570-90n<180,并且n为正整数,可求n的值,从而求解即可.
解答 解:设这个外角的度数是x°,则
(5-2)×180-(180-x)+x=600,
解得x=120.
故这个外角的度数是120°.
(2)存在.
设边数为n,这个外角的度数是x°,则
(n-2)×180-(180-x)+x=600,
整理得x=570-90n,
∵0<x<180,
即0<570-90n<180,并且n为正整数,
∴n=5或n=6.
故这个多边形的边数是6,这个外角的度数为30°.
点评 此题主要考查了多边形的内角和定理.关键是熟悉n边形的内角和为:180°•(n-2)的知识点.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:填空题
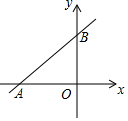 如图,直线AB分别交x轴,y轴于点A(-4,0),B(0,3),点C为y轴上的点,若以点C为圆心,CO长为半径的圆与直线AB相切时,则点C的坐标为(0,$\frac{4}{3}$)或(0,-12).
如图,直线AB分别交x轴,y轴于点A(-4,0),B(0,3),点C为y轴上的点,若以点C为圆心,CO长为半径的圆与直线AB相切时,则点C的坐标为(0,$\frac{4}{3}$)或(0,-12).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
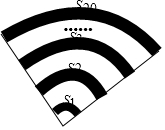 手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1,若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20=205π.
手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1,若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20=205π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com