
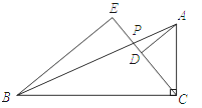
【题目】已知:如图,Rt△ABC中,∠ACB=90°,P是边AB上一点,AD⊥CP,BE⊥CP,垂足分别为D、E,已知AB=3![]() ,BC=3
,BC=3![]() ,BE=5.求DE的长.
,BE=5.求DE的长.
科目:初中数学 来源: 题型:
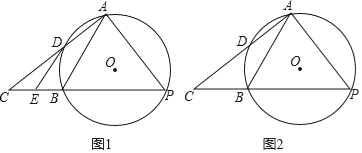
【题目】已知AB是⊙O的弦,点P是优弧AB上的一个动点,连接AP,过点A作AP的垂线,交PB的延长线于点C.
(1)如图1,AC与⊙O相交于点D,过点D作⊙O的切线,交PC于点E,若DE∥AB,求证:PA=PB;
(2)如图2,已知⊙O的半径为2,AB=2![]() .
.
①当点P在优弧AB上运动时,∠C的度数为 °;
②当点P在优弧AB上运动时,△ABP的面积随之变化,求△ABP面积的最大值;
③当点P在优弧AB上运动时,△ABC的面积随之变化,△ABC的面积的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角形的判定
(1)有一个角是________________的三角形是直角三角形.
(2)有两个角________________的三角形是直角三角形.
(3)勾股定理的逆定理:如果三角形两边的平方和等于________________,那么这个三角形是直角三角形.
(4)如果三角形一边上的________________等于这边的一半,那么这个三角形是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
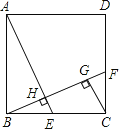
【题目】如图,在正方形ABCD中,E是BC上的一点,连结AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.
求证:(1) CG=BH;(2)FC2=BF·GF;(3)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(![]() ≈1.414,精确到1米)
≈1.414,精确到1米)
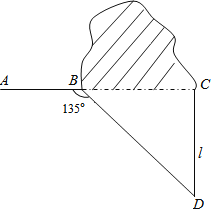
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列的解题过程,然后回答下列问题.
例:解绝对值方程:![]() .
.
解:讨论:①当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() ;
;
②当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
原方程的解为![]() 或
或![]() .
.
(1)依例题的解法,方程算![]() 的解是_______;
的解是_______;
(2)尝试解绝对值方程:![]() ;
;
(3)在理解绝对值方程解法的基础上,解方程:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com