
【题目】如图,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面三个结沦:①AS=AR:②QP∥AR;③△BRP≌△CSP.其中正确的是( )

A. ①③ B. ②③ C. ①② D. ①②③
 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】先化简再求值:当a=9时,求a+![]() 的值,甲乙两人的解答如下:
的值,甲乙两人的解答如下:
甲的解答为:原式=a+![]() =a+(1-a)=1.
=a+(1-a)=1.
乙的解答为:原式=a+![]() =a+(a-1)=2a-1=17.
=a+(a-1)=2a-1=17.
两种解答中,_____的解答是错误的,错误的原因是当a=9时______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(理解新知)
如图①,已知![]() ,在
,在![]() 内部画射线
内部画射线![]() ,得到三个角,分别为
,得到三个角,分别为![]() 、
、![]() 、
、![]() ,若这三个角中有一个角是另外一个角的2倍,则称射线
,若这三个角中有一个角是另外一个角的2倍,则称射线![]() 为
为![]() 的“2倍角线”
的“2倍角线”
(1)角的平分线 这个角的“2倍角线”;(填“是”或“不是”)
(2)若![]() ,射线
,射线![]() 为
为![]() 的“2倍角线”,则
的“2倍角线”,则![]()
![]() ;
;
(解决问题)
如图②,已知![]() ,射线
,射线![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 的速度绕
的速度绕![]() 点逆时针旋转:射线
点逆时针旋转:射线![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 的速度绕
的速度绕![]() 点顺时针旋转,射线
点顺时针旋转,射线![]() 、
、![]() 同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为
同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为![]() .
.
(3)当射线![]() 、
、![]() 旋转到同一条直线上时,求
旋转到同一条直线上时,求![]() 的值;
的值;
(4)若![]() 、
、![]() 、
、![]() 三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的
三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的![]() 的值.(本题中所研究的角都是小于等于
的值.(本题中所研究的角都是小于等于![]() 的角.)
的角.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=6,N为AB上一点,且AN=2,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM,MN,则BM+MN的最小值是( )
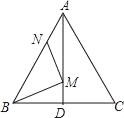
A. 8 B. 10 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】交警通常根据刹车后轮滑行的距离来测算车辆行驶的速度,所用的经验公式是u=16![]() .其中u表示车速(单位:km/h),d表示刹车距离(单位:m),f表示摩擦系数.在一次交通事故中,测得d=20m,f=1.44,而发生交通事故的路段限速为80km/h,肇事汽车是否违规超速行驶?说明理由.(参考数据:
.其中u表示车速(单位:km/h),d表示刹车距离(单位:m),f表示摩擦系数.在一次交通事故中,测得d=20m,f=1.44,而发生交通事故的路段限速为80km/h,肇事汽车是否违规超速行驶?说明理由.(参考数据:![]() ≈1.4,
≈1.4,![]() ≈2.2)
≈2.2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.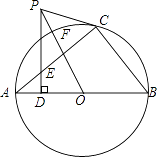
(1)求证:PC是⊙O的切线;
(2)若PC=3,PF=1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
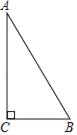
【题目】如图,在Rt△ABC中,∠C=90°,AC=4.
(1)若BC=2,求AB的长;
(2)若BC=a,AB=c,求代数式(c﹣2)2﹣(a+4)2+4(c+2a+3)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=(x-1)2-4,AB为半圆的直径,求这个“果圆”被y轴截得的弦CD的长 . 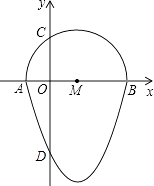
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com